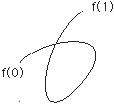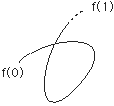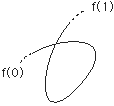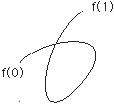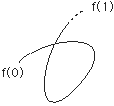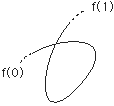- 「曲線」は,実数の区間から空間(n次元ユークリッド空間)の中への連続写像として定義されます。
特に,平面上の曲線とは,実数の区間から平面(2次元ユークリッド空間)の中への連続写像のことです。
| 両端が閉じた曲線
| 区間 [0,1] → 空間
| 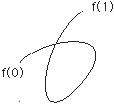
|
一端が閉じて
もう一端が開いた
曲線
| 区間 [0,1[ → 空間
| 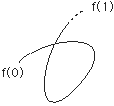
|
| 両端が開いた曲線
| 区間 ]0,1[ → 空間
| 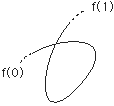
|
- この定義のアイデアは,曲線を運動の軌跡として表現するということです。
- 鉛筆で曲線を描いている場面を想像して下さい。鉛筆の運動が曲線となって現れます。t ∈ [0, 1] は,時間 (time) をイメージしています。0 が開始時間,1 が終了時間です。
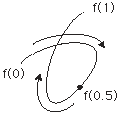
- つぎの二つの曲線は,像は同じですが,異なるものです:
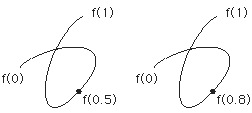
- 「曲線」のこの定義は,わたしたちが常識的に理解している「曲線」の形式化ですが,このように定義された曲線のうちには,わたしたちの常識を超える(外れる)ものも入ってきます。
- 例:ペアノ曲線
これは,正方形の中に「ぎっしり詰まっている」(言い換えると,「外目には正方形のように見える」)曲線です。