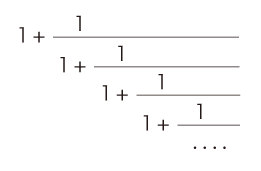
そこで,これの延長として,「つぎの連分数はどうなるんだろうか?」となりそうである。 
結論から言うと,これは 1+√2 になる。 以下に解説するが,√2 の連分数表現がつぎのようになる: 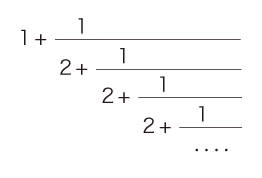 √2 の連分数表現は,ユークリッド互除法をつぎのように行うことで得られる: よって,√2の連分数表現として,つぎを得る: 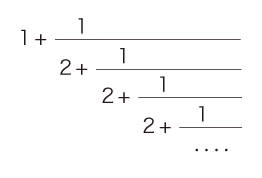 |
| Up | √2の 連分数表現 | 更新: 2014-07-22 |

そこで,これの延長として,「つぎの連分数はどうなるんだろうか?」となりそうである。 
結論から言うと,これは 1+√2 になる。 以下に解説するが,√2 の連分数表現がつぎのようになる: 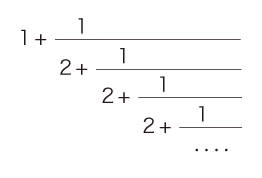 √2 の連分数表現は,ユークリッド互除法をつぎのように行うことで得られる: よって,√2の連分数表現として,つぎを得る: 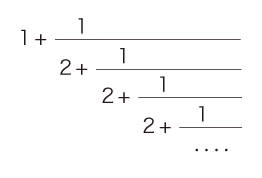 |