Up

フラクタル性 (自己相似形の生成)

作成: 2014-07-19 更新: 2014-07-22

---

黄金角は，線分の黄金比の，円周バージョンである。 そこで，黄金比のフラクタル性 (自己相似形の生成) に対し，これの黄金角バージョンを考えることになる。 さて，それはどんなふう？ 先ず， φ360゜＝ φ(φ2α) ＝ φ(1+φ)α＝φα+φ2α ＝ φα＋360゜ そこで， φα = 360゜−α φ2α = 360゜ φ3α ＝ φφ2α ＝ φ360゜ ＝ φα＋360゜ φ4α = φ(φ3α) ＝ φ(φα＋360゜) = φ2α＋φ360゜= 360゜＋φα＋360゜= φα＋2・360゜ φ5α = φ(φ4α) ＝ φ(φα＋2・360゜) = φ2α＋2φ360゜＝360゜+2(φα＋360゜) = 2φα+3・360゜ φ6α = φ(φ5α) ＝ φ(2φα+3・360゜) = 2φ2α+3φ360゜＝2・360゜+3(φα＋360゜) = 3φα+5・360゜ φ7α = φ(φ6α) ＝ φ(3φα+5・360゜) = 3φ2α+5φ360゜＝3・360゜+5(φα＋360゜) = 5φα+8・360゜ φ8α = φ(φ7α) ＝ φ(5φα+8・360゜) = 5φ2α+8φ360゜＝5・360゜+8(φα＋360゜) = 8φα+13・360゜ 　‥‥‥‥ よって， φα = 360゜−α ≡ −α (mod 360゜) 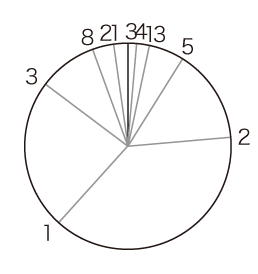φ2α = 360゜≡ 0 (mod 360゜) φ3α ＝ φα＋360゜≡ φα ≡ −α (mod 360゜) φ4α = φα+2・360゜≡ φα ≡ −α (mod 360゜) φ5α = 2φα+3・360゜≡ 2φα ≡ −2α (mod 360゜) φ6α = 3φα+5・360゜ ≡ 3φα ≡ −3α (mod 360゜) φ7α = 5φα+8・360゜ ≡ 5φα ≡ −5α (mod 360゜) φ8α = 8φα+13・360゜ ≡ 8φα ≡ −8α (mod 360゜) 　‥‥‥‥ こうして，黄金比のフラクタル性の黄金角バージョンは，つぎのようになる： 《角度 −α を単位にして，円周上でフィボナッチ数跳びをする》 　　 1：138゜ 2：275゜ 3：53゜ 5：328゜ 8：20゜ 13：348゜ 21：8゜ 34：355゜ 55：3゜ 89：358゜ ‥‥ 上図に示されるように，０゜(mod 360゜) への収束プロセスが，黄金角のフラクタル性ということになるわけである。