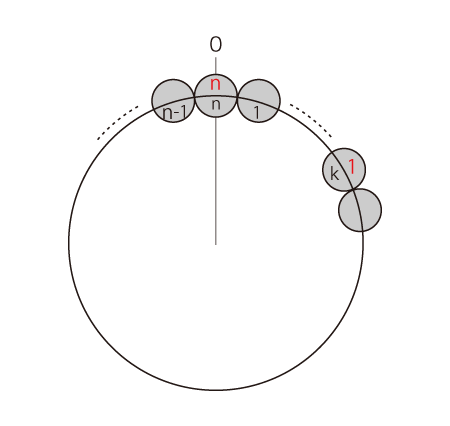
つぎの問題を考える:
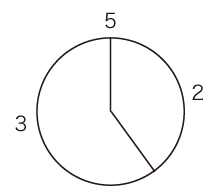
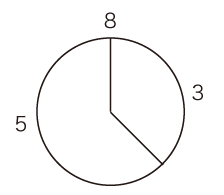
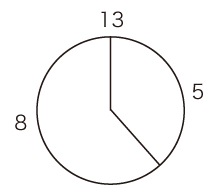
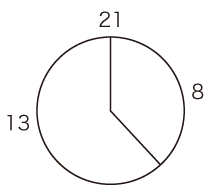
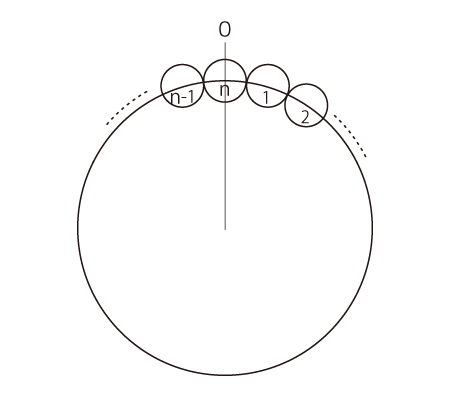
- 円周に,要素n個をきっちり並べる。
- 配置の方法は,「Oからスタートして,k跳びで要素を置いていく」。
- さらに,「k跳びをn回やったとき,要素n個の配置がちょうど成っている」が条件。
──特に,以上の要件より,Oの位置に<n回目>がくる(註1)。
勝手に選んだn,kでは,こうはならない。
一方これが成り立つようなn,kは,格別なものでもない。
即ち,互いに素な2つの数であればよい(註2)。
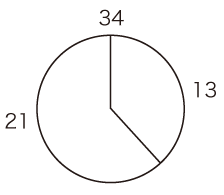
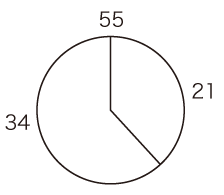
フィボナッチ数列だと,Fn+2 と Fn が互いに素(註3)であるから,(5, 2), (8,3), (13, 5), (21, 8), (34, 13), (55, 21) ‥‥ の組で,成り立つ。
上図で,小さい数の側の角は,これの極限が黄金角であり,それ自身も黄金角と近い。
そこで,開始点Oから黄金角i回転に対応する円周上の点に数iを置いていくとき,つぎのことが成り立つ:
- 各フィボナッチ数n( =5, 8, 13, 21, 34, 55, ‥‥ ) に対し,黄金角のn回の回転で,円周にn個がほぼ等間隔に並ぶ。
- 開始点Oの付近に,フィボナッチ数が並ぶ(註4)。
- 異なる2数の位置は,重ならない(註5)。
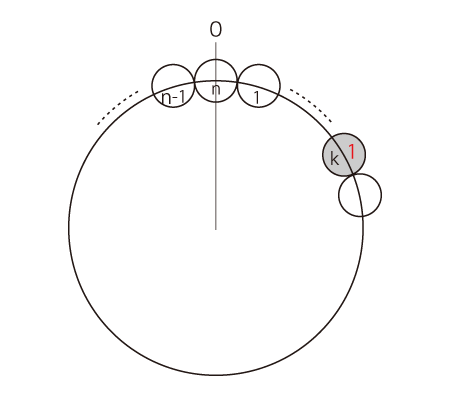
| 註1 : |
nより小さいiでi回目にOの位置にきたときは,(i+1)回目が1回目と重なる。
|
| 註2 : |
nより小さいi<jで,k跳びi回とj回が重なるとする。
即ち,k×(jーi) =n×p となる整数pが存在するとする。
kとnが互いに素であれば,kはpの因子。
そしてこのときは jーi>nになり,矛盾。
|
| 註3 : |
Fn+2 = Fn+1 + Fn より,Fn+2 と Fn がpを共通因子とするとき,Fn+1 もpを因子にする。
これは,「5,2,3はpを共通因子とする」に溯行し,矛盾。
|
| 註4 : |
ちなみに,位置はつぎのようになる:
5 : 左 32.5゜
8 : 右 20.1゜
13 : 左 12.4゜
21 : 右 7.7゜
34 : 左 4.7゜
55 : 右 2.9゜
89 : 左 1.8゜
|
| 註5 : |
重なるとは,黄金角のある整数倍が 360゜の整数倍になること。これは,黄金角と360゜の比 1/φ2 = 1/(1+φ) が有理数だということ,特に φが有理数だということ。
一方,φの連分数表現が直接証明になるように,φは無理数。
|
|