- 「正多角形」の意味づけは,「回転対称な多角形」──すなわち,つぎの条件を満たす〈回転の中心〉をもつ多角形──です:
各頂点が隣の頂点の位置に移動する
この〈回転の中心〉を,正多角形の「中心」と呼ぶことにします。
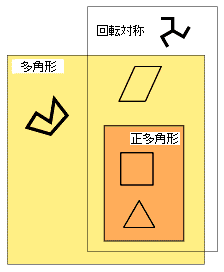
- 「正多角形」では:
- 内角の二等分線は回転の中心で交わります。また,線対称の軸になります。
- 回転の中心は,外接円の中心です。実際,中心と頂点を結ぶ線分が半径になります。
- 辺の垂直二等分線は回転の中心で交わります。また,線対称の軸になります。
- 回転の中心は,内接円の中心です。実際,中心から辺に下ろした垂線が半径になります。
- 「円」は「正無限角形」と見なすことができます。そして,「円の中心」は正無限角形の中心と見なせます。
|

