Up | English

2つの(合同な)図形の対称な位置関係

---

• 「2点の対称な位置関係」と「自己対称形」の概念の間には，かなりギャップがあります。
  そこで，この間に「2つの(合同な)図形の対称な位置関係」の概念を挿むことにします。
  
  
  
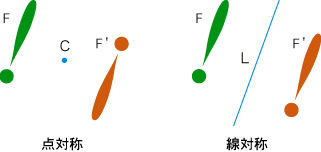
• ２つの図形は，点を鏡として互いに他の像になっているとき,「点対称」であるといいます。
  
  
  ここで,「２つの図形Ｆ, Ｆ' は点Ｃを鏡として互いに他の像になっている」とは，
  一方の図形の各点Ｐに対し，Ｃに関してＰと対称な点が，他方の図形の点になっている
  ということです。(「Ｆ, Ｆ' は点Ｃに関して互いに対称」と言います。)
  
  
  
• 同様に，２つの図形は，直線を鏡として互いに他の像になっているとき,「線対称」であるといいます。
  
  
  ここで,「２つの図形Ｆ, Ｆ' は直線Ｌを鏡として互いに他の像になっている」とは，
  一方の図形の各点Ｐに対し，Ｌに関してＰと対称な点が，他方の図形の点になっている
  ということです。(「Ｆ, Ｆ' は直線Ｌに関して互いに対称」と言います。)

• 対称な位置関係にある２つの図形は，合同です。