そして,この「独特」をつくっている特徴の最も大きなものが,「測度 (measure)」がないということである。 幾何学に「測度」がないことは,不都合であり,そもそも異常である。 実際,幾何学は「測度」無しには済まない。 では,ユークリッド幾何学は,「測度」をどのように処理しているのか? 「三角形・円」で代用しているのである。 実際,ユークリッド幾何学の「三角形・円」の話を素直に「三角形・円」の話として受け取っていたら,間違いである。 多くの場合,それは「測度」の話である。 「三角形・円」が「測度」の代わりに用いられるということから,自明/簡単な命題の証明に大きな定理が使われるという事態に,しばしば出会うことになる。 そしてこのときには,循環論法を犯しているのではないかと,危ぶむことになる。 例として,つぎの命題を考える:
この証明は,つぎのようになる:
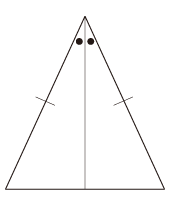
よって,もとの二等辺三角形の底角は等しい。 あるいは,つぎのようになる:
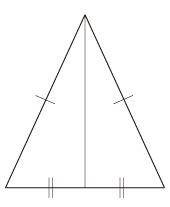
よって,もとの二等辺三角形の底角は等しい。 ここで,つぎの素朴な疑問になる:
「二等辺三角形の底角は等しい」は,「線分の長さ」「角の大きさ」の「測度」が主題である。 しかし,ユークリッド幾何学は「測度」をもたない。 「測度」に依らずに線分の長さ,角の大きさの相等・相違を導くのに,「三角形の合同」を用いる。 別の命題の証明では,これと同様の趣旨で,「円」が登場してくる。 これがユークリッド幾何学というものであるが,現代数学の方から見れば,どうしても「倒錯」を見てしまう。 しかし,この「倒錯」こそが,ユークリッド幾何学であり,ユークリッド幾何学の真骨頂なのである。
|
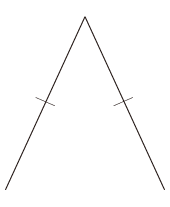
 「直角三角形の3頂点は,直角の対辺の中点から等距離」
「直角三角形の3頂点は,直角の対辺の中点から等距離」