Up 先決問題 :「点の位相」
更新: 2015-12-17

    ここまでは，「同形の変形を表している点対応」を「同形の点対応」と言ってきた。
    そして「同形の変形」は，実物操作ないしそれのイメージである。

    「同形の点対応」は，つぎのように言えなければ，数学にならない：
      「同形の点対応は，これこれの条件を満たす関数」
    そこで，これを言えるようになることを，いまからの課題としよう。


    探索：
    つぎは，同形である：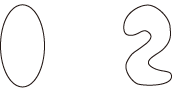
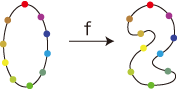
    説明の仕方：「つぎが，同形の点対応になる」：

    つぎは，同形の点対応が存在しない：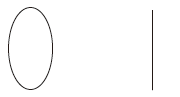
    説明の仕方：「端点に写る点は，端点に限る」

    つぎも，同形の点対応が存在しない：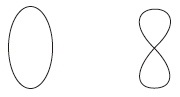
    説明の仕方：「四叉路交差点に写る点は，四叉路交差点に限る」

    しかし，「端点」「四叉路交差点」のような言い方をしたら，きりがない。
    欲しいのは，一般的な言い方である。
    そしてこのとき，つぎのことに気づく：
      「同形」の表現では，点の位相 (位置の相) の表現が要る。
      そして，点の位相の表現は，形全体の同形の表現から独立。
    実際，つぎの図において
      P，Qは，同じ形の２点だが，位相が違う
      P，P′ は，同形でない図形の２点だが，位相が同じ
      Q，Q′ は，同形でない図形の２点だが，位相が同じ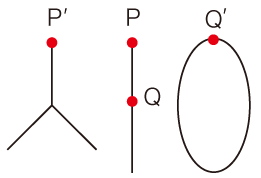