| \[
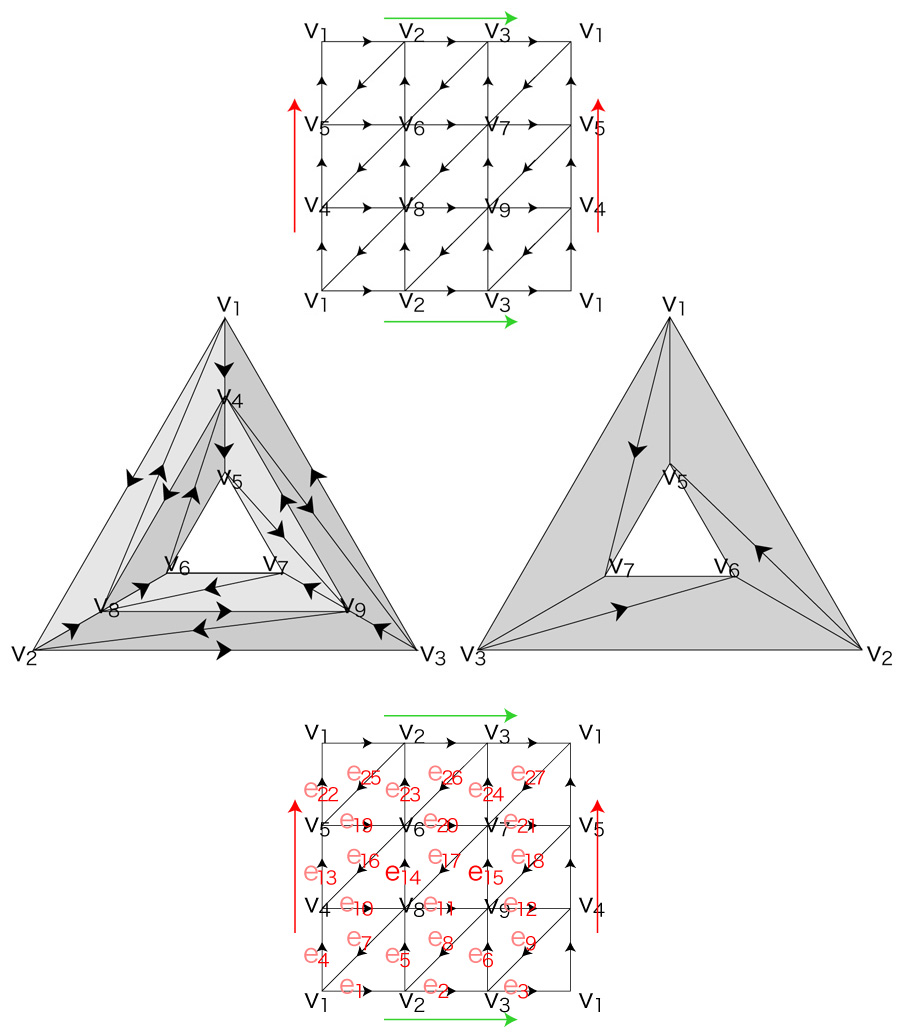
e_1 = [ 1,\ 2 ] \\
e_2 = [ 2,\ 3 ] \\
e_3 = [ 3,\ 1 ] \\
\ \\
e_4 = [ 1,\ 4 ] \\
e_5 = [ 2,\ 8 ] \\
e_6 = [ 3,\ 9 ] \\
\ \\
e_7 = [ 8,\ 1 ] \\
e_8 = [ 9,\ 2 ] \\
e_9 = [ 4,\ 3 ] \\
\] |
\[
e_{10} = [ 4,\ 8 ] \\
e_{11} = [ 8,\ 9 ] \\
e_{12} = [ 9,\ 4 ] \\
\ \\
e_{13} = [ 4,\ 5 ] \\
e_{14} = [ 8,\ 6 ] \\
e_{15} = [ 9,\ 7 ] \\
\ \\
e_{16} = [ 6,\ 4 ] \\
e_{17} = [ 7,\ 8 ] \\
e_{18} = [ 5,\ 9 ] \\
\] |
\[
e_{19} = [ 5,\ 6 ] \\
e_{20} = [ 6,\ 7 ] \\
e_{21} = [ 7,\ 5 ] \\
\ \\
e_{22} = [ 5,\ 1 ] \\
e_{23} = [ 6,\ 2 ] \\
e_{24} = [ 7,\ 3 ] \\
\ \\
e_{25} = [ 2,\ 5 ] \\
e_{26} = [ 3,\ 6 ] \\
e_{27} = [ 1,\ 7 ]
\] |