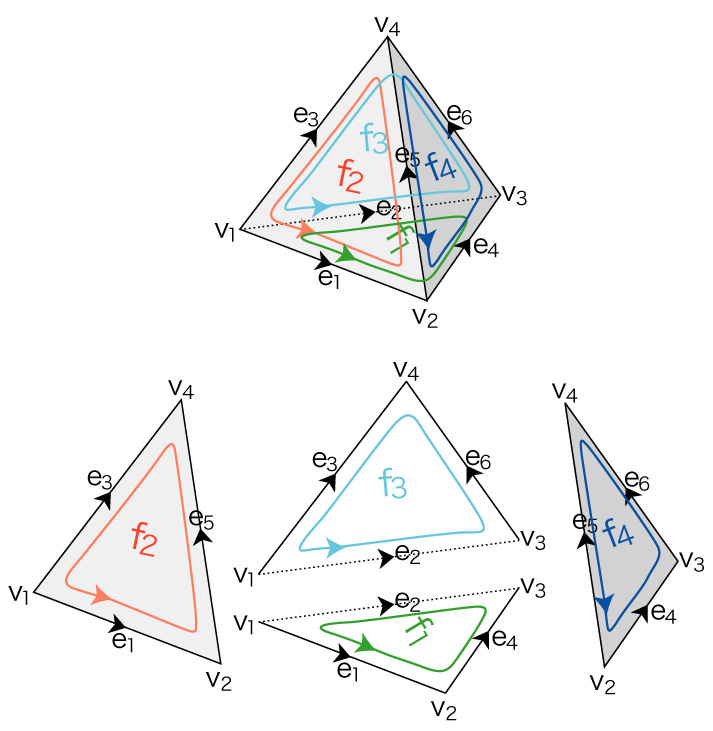
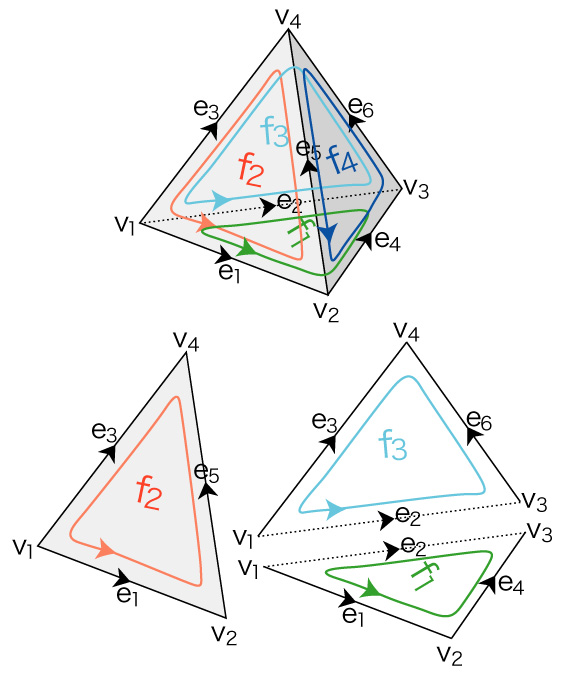
\( C_1 \) の基底は,\( \{ e_1, e_2, e_3, e_4, e_5, e_6 \} \) をとる。
各 \( f_k \) のバウンダリは,
\[
\begin{align}
\partial f_1 = e_1 + e_4 - e_2 =\ & e_1 & - e_2 & & + e_4 & &\\
\partial f_2 = e_1 + e_5 - e_3=\ & e_1 & & - e_3 & & + e_5 & \\
\partial f_3 = e_2 + e_6 - e_3 =\ & & e _2 & - e_3 & & & + e_6 \\
\partial f_4 = e_4 + e_6 - e_5 =\ & & & & e_4 & - e_5 & + e_8 \\
\end{align}
\]
よって,基底 \( \{ f_k\}, \{ e_i \} \) に対する \( \partial_2 : C_2 \rightarrow C_1 \) の表現行列は,
\[
\begin{align}
\begin{array}{c c}
& \begin{array} {@{} c c c c @{}}
\ \ \ e_1 & e_2 & e_3 & e_4 & e_5 & e_6
\end{array} \\
\begin{array}{c}
f_1 \\ f_2 \\ f_3 \\ f_4
\end{array}
\hspace{-1em} &
\left(
\begin{array}{@{} c c c c c c @{}}
& 1 & -1 & & 1 & & \ \ \ \\
& 1 & & -1 & & 1 & \\
& & 1 & -1 & & & 1 \\
& & & & 1 & -1 & 1 \\
\end{array}
\right) \\
\mbox{} % Blank line to match column names so as to align the = vertically
\end{array} \\[-12pt] % Correction for blank line
\end{align}
\]
これに対し
\( f'_4 = f_4 - f_3 \)
\[
\begin{align}
\begin{array}{c c}
& \begin{array} {@{} c c c c @{}}
\ \ \ e_1 & e_2 & e_3 & e_4 & e_5 & e_6
\end{array} \\
\begin{array}{c}
f_1 \\ f_2 \\ f_3 \\ f'_4
\end{array}
\hspace{-1em} &
\left(
\begin{array}{@{} c c c c c c @{}}
& 1 & -1 & & 1 & & \ \ \ \\
& 1 & & -1 & & 1 & \\
& & 1 & -1 & & & 1 \\
& & -1 & 1 & 1 & -1 & \\
\end{array}
\right) \\
\mbox{} % Blank line to match column names so as to align the = vertically
\end{array} \\[-12pt] % Correction for blank line
\end{align}
\]
\( f''_4 = f'_4 + f_2 \)
\[
\begin{align}
\begin{array}{c c}
& \begin{array} {@{} c c c c @{}}
\ \ \ e_1 & e_2 & e_3 & e_4 & e_5 & e_6
\end{array} \\
\begin{array}{c}
f_1 \\ f_2 \\ f_3 \\ f''_4
\end{array}
\hspace{-1em} &
\left(
\begin{array}{@{} c c c c c c @{}}
& 1 & -1 & & 1 & & \ \ \ \\
& 1 & & -1 & & 1 & \\
& & 1 & -1 & & & 1 \\
& 1 & -1 & & 1 & & \\
\end{array}
\right) \\
\mbox{} % Blank line to match column names so as to align the = vertically
\end{array} \\[-12pt] % Correction for blank line
\end{align}
\]
\( f'''_4 = f''_4 - f_1 \)
\[
\begin{align}
\begin{array}{c c}
& \begin{array} {@{} c c c c @{}}
\ \ \ e_1 & e_2 & e_3 & e_4 & e_5 & e_6
\end{array} \\
\begin{array}{c}
f_1 \\ f_2 \\ f_3 \\ f'''_4
\end{array}
\hspace{-1em} &
\left(
\begin{array}{@{} c c c c c c @{}}
& 1 & -1 & & 1 & & \ \ \ \\
& 1 & & -1 & & 1 & \\
& & 1 & -1 & & & 1 \\
& & & & & & \\
\end{array}
\right) \\
\mbox{} % Blank line to match column names so as to align the = vertically
\end{array} \\[-12pt] % Correction for blank line
\end{align}
\]
この行列は,つぎのことを示している:
\( Im( \partial_2 ) \) は3次元。
実際,つぎの3つのバウンダリサイクルがこれの基底を成す:
\[
\partial f_1 = e_1 + e_4 - e_2 \\
\partial f_2 = e_1 + e_5 - e_3 \\
\partial f_3 = e_2 + e_6 - e_3 \\
\]
|