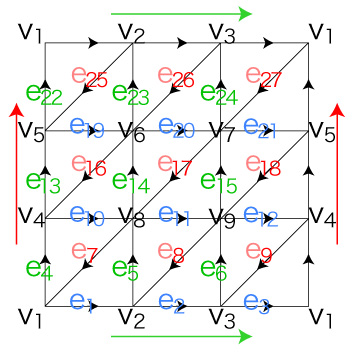
各 \( f_k \) のバウンダリは,
\[
\partial_2 f_{1} = e_{1} + e_{5} + e_{7} \\
\partial_2 f_{2} = e_{2} + e_{6} + e_{8} \\
\partial_2 f_{3} = e_{3} + e_{4} + e_{9} \\
\partial_2 f_{4} = e_{4} + e_{10} + e_{7} \\
\partial_2 f_{5} = e_{5} + e_{11} + e_{8} \\
\partial_2 f_{6} = e_{6} + e_{12} + e_{9} \\
\partial_2 f_{7} = e_{10} + e_{14} + e_{16} \\
\partial_2 f_{8} = e_{11} + e_{15} + e_{17} \\
\partial_2 f_{9} = e_{12} + e_{13} + e_{18} \\
\partial_2 f_{10} = e_{13} + e_{19} + e_{16} \\
\partial_2 f_{11} = e_{14} + e_{20} + e_{17} \\
\partial_2 f_{12} = e_{15} + e_{21} + e_{18} \\
\partial_2 f_{13} = e_{19} + e_{23} + e_{25} \\
\partial_2 f_{14} = e_{20} + e_{24} + e_{26} \\
\partial_2 f_{15} = e_{21} + e_{22} + e_{27} \\
\partial_2 f_{16} = e_{22} + e_{1} + e_{25} \\
\partial_2 f_{17} = e_{23} + e_{2} + e_{26} \\
\partial_2 f_{18} = e_{24} + e_{3} + e_{27} \\
\]
よって,基底 \( \{ f_k\}, \{ e_i \} \) に対する \( \partial_2 : C_2 \rightarrow C_1 \) の表現行列は,
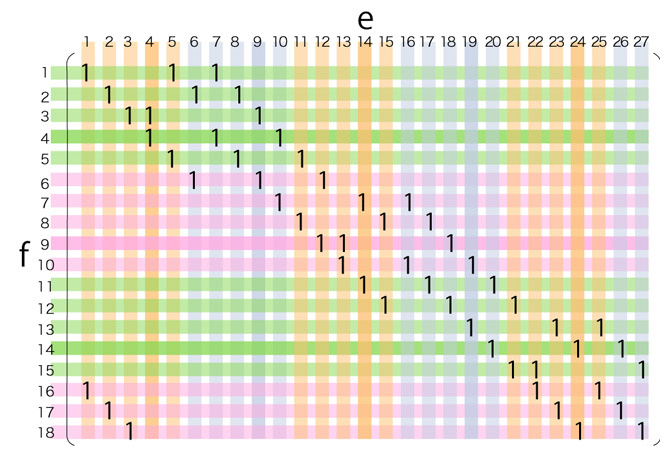
\( \partial_2 \) によって潰れる次元は,ほとんど無いように見える。
\( f_{15}^{(1)} = f_{15} - f_{18} \)
\( f_{14}^{(1)} = f_{14} - f_{17} \)
\( f_{13}^{(1)} = f_{13} - f_{16} \)
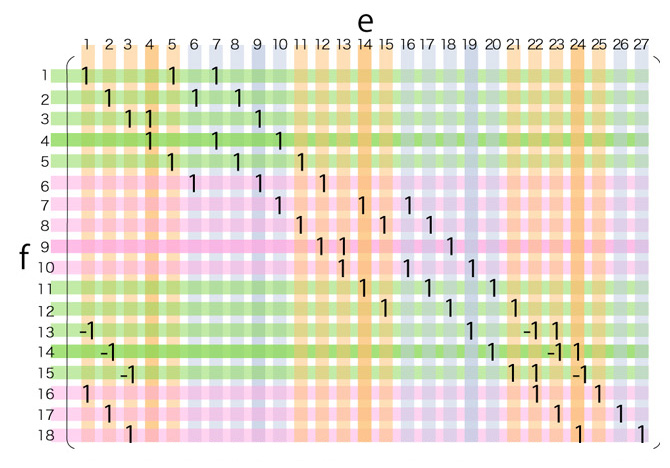
\( f_{14}^{(2)} = f_{14}^{(1)} + ( f_{15}^{(1)} + f_{13}^{(1)} ) \)
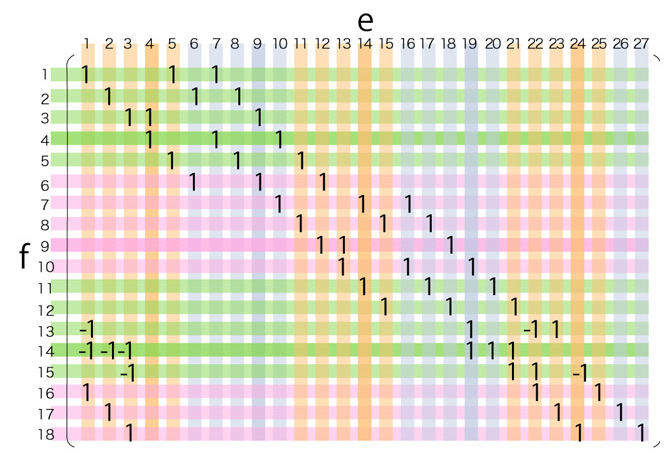
\( f_{14}^{(3)} = f_{14}^{(2)} - ( f_{12} + f_{11} + f_{10} ) \)
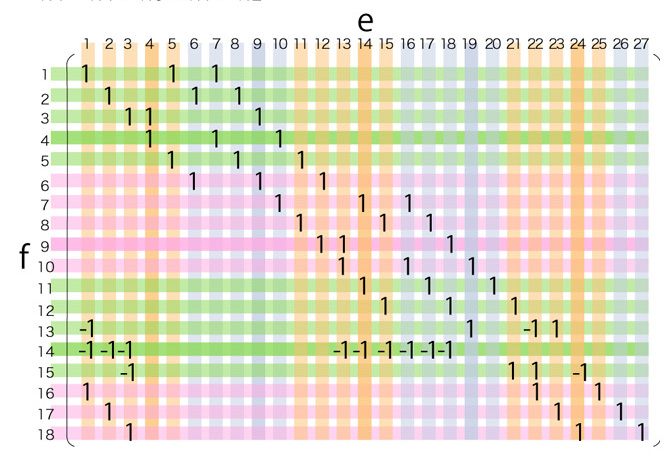
\( f_{14}^{(4)} = f_{14}^{(3)} + ( f_{9} + f_{8} + f_{7} ) \)
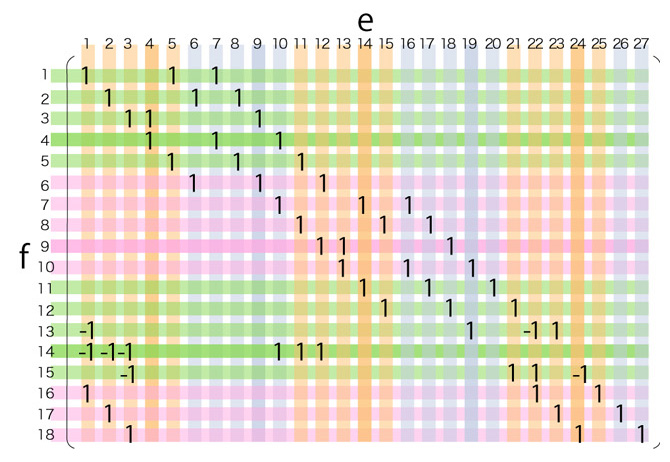
\( f_{14}^{(5)} = f_{14}^{(4)} - ( f_{6} + f_{5} + f_{4} ) \)
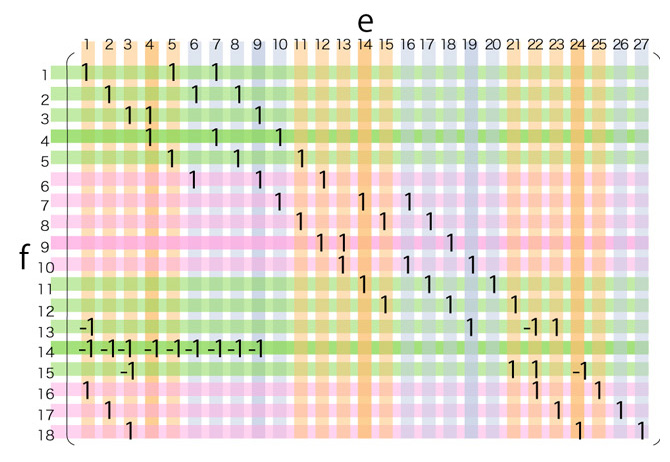
\( f_{14}^{(6)} = f_{14}^{(5)} + ( f_{3} + f_{2} + f_{1} ) \)
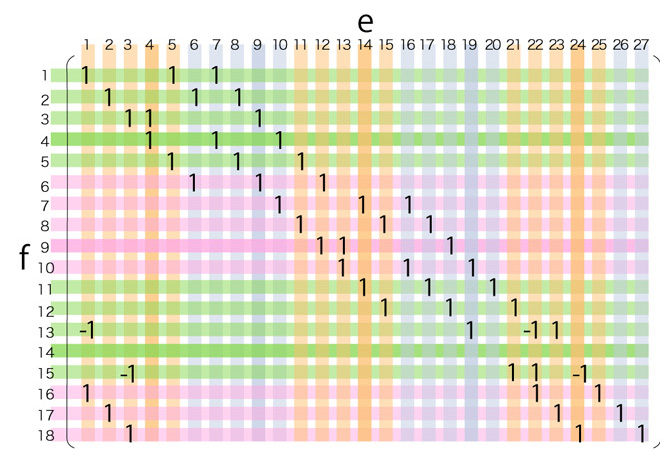
最後の行列は,つぎを示している:
\( \partial_2 f_{ 15 }\ \) を除いた 17個のバウンダリサイクル \( \partial_2 f_{ 1 }, \cdots\ , \partial_2 f_{ 14 },\ \partial_2 f_{ 16 },\ \partial_2 f_{ 17 },\ \partial_2 f_{ 18 }\ \) が,\( Im( \partial_2 ) \) の基底を成す。
特に,\( Im( \partial_2 ) \) は 17次元。
|