- 多角形に関して「角(かく)」のことばが使われるとき,それにはつぎの2通りがあります:
- 角(かど)
- 角(かど) をなす2辺の開き (角度)
この2つは区別する必要があります。
──この区別の必要性は,多角形 (2次元) の3次元版である多面形を扱う段になると,わかります:
多面形では,「角(かど)」の概念は立つが,
「角(かど) をなす複数の面の開き (角度)」の概念は立たない。
実際,「角度」は,「端点を同じくする2本の線分/半直線の組」に関して立つ概念です。
( 角度) 角度)
- 生活感覚の「角(かど)」は,1点(先端)でのローカルな形状です。
先端をいくら拡大しても同じ形状が見えるというところに,「角(かど)」の特徴があります。
「角(かど)」はグローバルな形ではなく,先端の近傍の特徴であると言えます。
この感覚を「角(かど)」の定義に反映させようとしたら,かなりめんどうな定義になります。
そこで,ここでは簡単のため,「角(かど)」を「多角形・多面形の角(かど)」のことにして,これをグローバルな形状として定義して済ませることにします。
(「角(かど)」の印象は「ローカル」ですが,定義では記述の便宜から「グローバル」をとることにします。)
すなわち,多角形・多面形の「角(かど)」を,以下のように定義することにします。
- 多角形 (頂点・辺で構成される形として) の場合,一つの頂点を共有する辺の組を「角(かど)」と定義する:
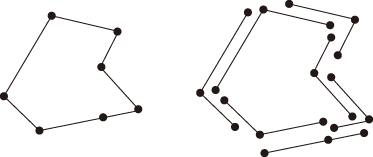
(左の多角形のすべての角(かど) を取り出したのが,右)
特に,角は,尖った形である必要はありません。
つぎの角は「平角(へいかく)」と呼ばれます:


(左の多面形の角(かど) を一つ取り出したのが,右)
|





