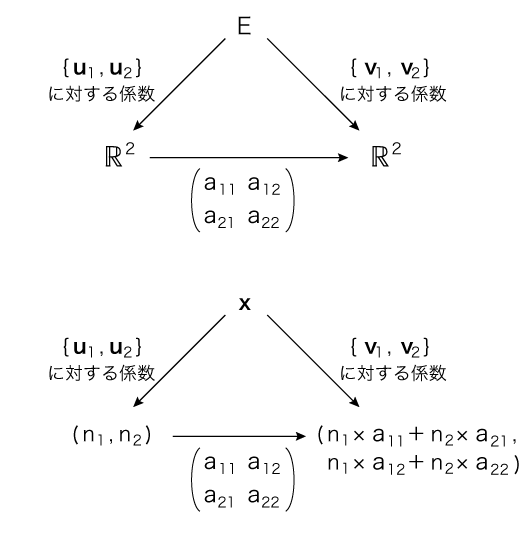
Up 基底変換によるベクトルの新表現の計算が,「行列の作用」に  

    基底変換によるベクトルの新表現は，つぎのように定まる。
    {ｕ1, ｕ2}, {ｖ1, ｖ2} が線型空間Ｅの２つの基底であり，ｕ1, ｕ2 の {ｖ1, ｖ2} に対する表現がつぎのようであるとする：
        ｕ1 ＝ ｖ1 × ａ11 ＋ ｖ2 × ａ12
        ｕ2 ＝ ｖ1 × ａ21 ＋ ｖ2 × ａ22
    ここでベクトルｘの基底 {ｕ1, ｕ2} に対する表現が
        ｘ＝ ｕ1 × ｎ1 ＋ ｕ2 × ｎ2
    であるとき，ｘの基底 {ｖ1, ｖ2} に対する表現はつぎのようになる：
        ｘ＝ ｖ1 × ( ｎ1 × ａ11 ＋ ｎ2 × ａ21 )
        　＋ ｖ2 × ( ｎ1 × ａ12 ＋ ｎ2 × ａ22 )

    そこで，{ｕ1, ｕ2} から {ｖ1, ｖ2} への基底変更にともなうベクトルの新表現を求める計算を，つぎのように定めればよいことになる：
      (ｎ1, ｎ2) ＝ ( ｎ1 × ａ11 ＋ ｎ2 × ａ21 , ｎ1 × ａ12＋ ｎ2 × ａ22 )

    これは，つぎの図式が可換であるように「行列の作用」を定義していることになる：