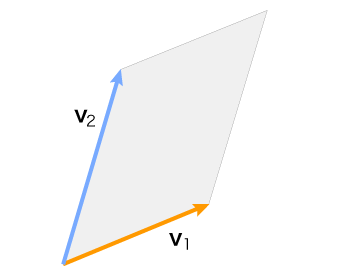
二つのベクトルv1, v1 が張る平行四辺形の面積を考える:
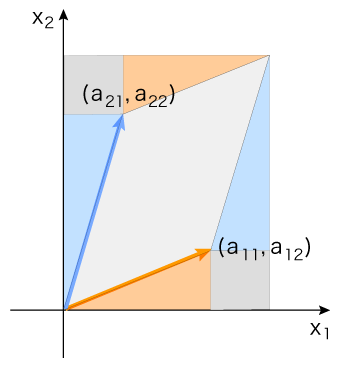
(a11 + a21 )
× (a12 + a22 )
ー( a11 × a12
+ a21 × a22
+ 2 × (a12 × a21) )
= a11 × a22
ー a12 × a21
|
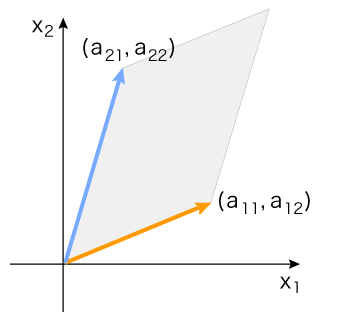
いま,ベクトル (a11, a12 ) と (a21, a22 ) が張る平行四辺形の面積を
 det( (a11, a12 ), (a21, a22 ) )
det( (a11, a12 ), (a21, a22 ) )
で表すことにする。
この記号法を,「行列式」と呼ぶ。
上の計算より,行列式 det( (a11, a12 ), (a21, a22 ) ) はつぎのように定義することになる:
 |
= a11 × a22
ー a12 × a21 |
しかし,ここに一つ問題が生じる。
ベクトル (a11, a12 ) と (a21, a22 ) が張る平行四辺形の面積は,ベクトル (a21, a22 ) と (a11, a12 ) が張る平行四辺形の面積を表すところの

と同じであり,そして上の定義に従えば,つぎのようになる:
 |
= a21 × a12
ー a22 × a11 |
符合が互いに逆の面積が2つ導かれてくるわけである。
この問題は,つぎのように定めることで,解決される:
《行列式が定める「平行四辺形の面積」は,符合のついた平行四辺形の面積》
即ち,行列式 det( (a11, a12 ), (a21, a22 ) ) の値の正負は,つぎのようになる:
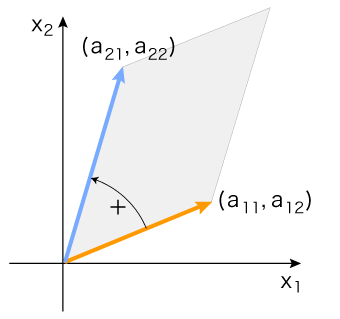
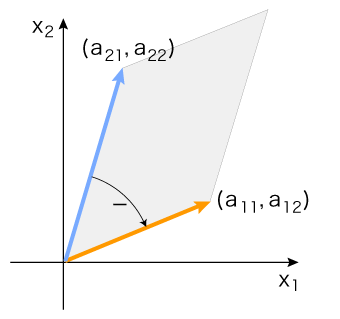
平行四辺形の中を,原点中心に,(a11, a12 ) を (a21, a22 ) に向けて回転する。
回転方向の正負 (反時計回りが正) が,det( (a11, a12 ), (a21, a22 ) ) の値の正負。
 | の場合, |
det( (a11, a12 ), (a21, a22 ) ) は,正値
|
det( (a21, a22 ), (a11, a12 ) ) は,負値
|
さて,「行列式は平行四辺形の面積」は,3次元では「行列式は平行六面体の体積」になる。
「平行四辺形の面積」はつぎの方法で導いたが,これはわかりやすいようにということで用いた方法であって,「平行六面体の体積」に延長できる方法ではない:

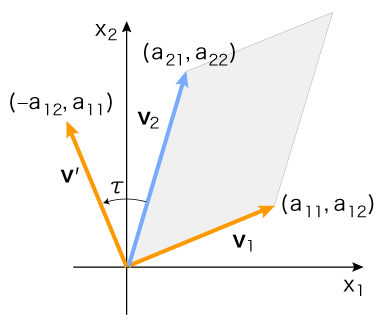
- 平行四辺形の面積は,底と定めた辺の長さと,この底に対して決まる高さで,求まる。
- 平行四辺形の底として,v1 をとる。
- これに対する高さは,つぎのベクトルと同じ方向を向く:
- v′ とv2 のなす角をτとするとき,
高さ = |v2| cosτ
cosτ = (v′ , v2 )
/ ( |v′ | |v2 | )
= (v′ , v2 )
/ ( |v1 | |v2 | )
よって,
- 「底の長さ = |v1| 」と「高さ = (v′ , v2 ) / |v1| 」より,
- (v′ , v2 ) をベクトルの成分で表す:
(v′ , v2 )
= ( ( ーa12, a11 ),
( a21, a22 ) ),
= a11 a22
ー a12 a21
|








