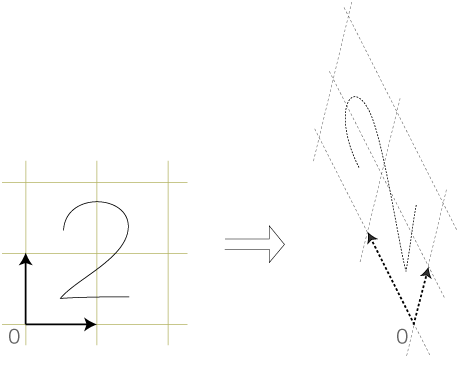
Up 「同形」を＜同型対応＞で捉える──「合同 → 相似 → ‥‥」の流れ  

    「線型写像」は，幾何学的に解釈することもできて，このときそれは
        「合同・相似」の概念の延長
    ということになります：

      平面ＰとＱの上に同じ図形Ａがある。
      この二つのAを視る。

    1. つぎの条件で二つのＡを見る：
        1. ＰとＱが，視線と垂直
        2. ＰとＱが，目から等距離
      このときの二つのＡのいろいろな見え方を，互いに同形と考える。 そして，この同形を「合同」と呼ぶ。


    2. つぎに，条件 a だけにしたときの二つのＡのいろいろな見え方を，互いに同形と考える。 そして，この同形を「相似」と呼ぶ。


    3. さらに，条件 a もなくしたときの二つのＡのいろいろな見え方を，互いに同形と考える。



    ３番目の同形に対しては，「合同・相似」のような呼び名は特にありません。
    この同形は，「線型空間の２つの部分集合の間の同型」にあたります。 そして，「線型写像」を使って数学的に定式化することになります。

    この数学的定式化では，同型対応のイメージがつぎのようになります：



    　註 : 厳密には，この場合「アフィン空間」の概念を導入する必要があります。
    実際，線型空間の要素は「ベクトル」であって，図形の要素となる「点」ではありません。「点」を要素とする空間は，アフィン空間ということになります。
    しかし，アフィン空間の導入は，話を複雑にしてしまいます。よって，アフィン空間と線型空間を一緒くたにしてしまう「方便」を，ここでは用いることにします。