「線型写像」はつぎのように定義される:
線型空間Eに対する関数f: E → F が線型写像であるとは,つぎの条件を満たすこと:
f( q × n ) = f( q ) × n
f( q + r ) = f( q ) + f( r )
|
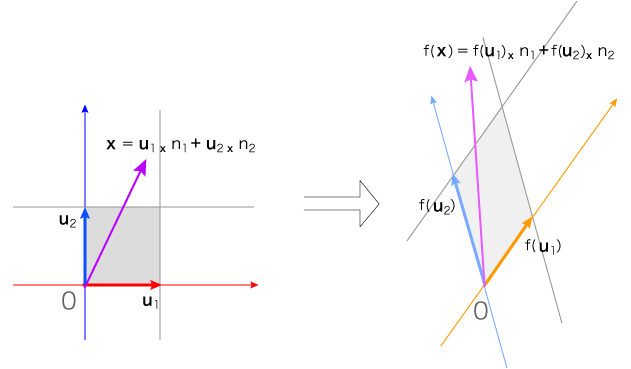
線型写像fは,基底 {u1, u2} の行き先f(u1), f(u2) で決まってしまう。
実際,x=
u1
×
n1
+
u2
×
n2
に対し,
f(x) = f(
u1
×
n1
+
u2
×
n2
)
= f(
u1
×
n1
)
+f(
u2
×
n2
)
= f(
u1
)
×
n1
+f(
u2
)
×
n2
|
ここで,Fの基底 {v1, v2} に対し
f(u1)
=
v1
×
a11
+
v2
×
a12
f(u2)
=
v1
×
a21
+
v2
×
a22
|
として,上の計算をさらに進めると,つぎのようになる:
=
(
v1
×
a11
+
v2
×
a12
)
×
n1
+
(
v1
×
a21
+
v2
×
a22
)
×
n2
=
(
(
v1
×
a11
)
×
n1
+
(
v2
×
a12
)
×
n1
)
+
(
(v1
×
a21
)
×
n2
+
(
v2
×
a22
)
×
n2
)
=
(
v1
×
(
a11
×
n1
)
+
v2
×
(
a12
×
n1
)
)
+
(
v1
×
(
a21
×
n2
)
+
v2
×
(
a22
×
n2
)
)
=
v1
×
(
n1
×
a11
+
n2
×
a21
)
+
v2
×
(
n1
×
a12
+
n2
×
a22
)
|
fが a11, a12, a21, a22 の4つの数で決まることがわかったので,「Eの基底 {u1, u2} とFの基底 {v1, u2} に対する線型写像fの表現」としてつぎの記号法を導入する (「行列」の登場!):
|