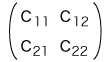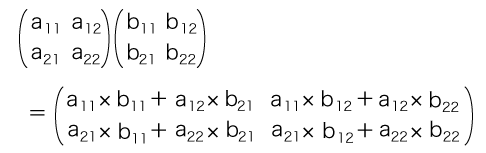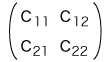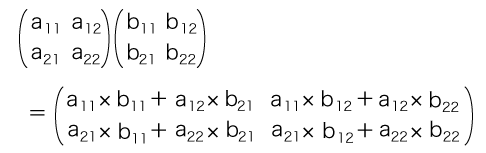線型空間E, F, G,線型写像f,g,Eの基底 {u1, u2},Fの基底 {v1, v2},Gの基底 {w1, w2} に関して,つぎの図式が可換であるとする:
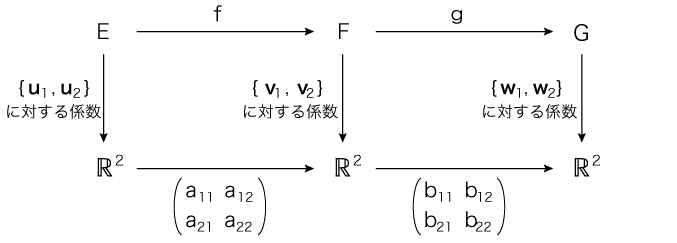
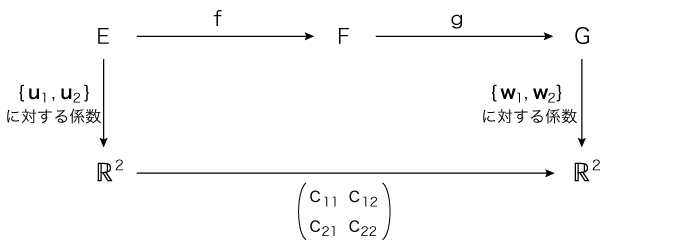
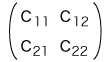
を求めることにする。
先ず,与条件として:
f(u1) =
v1
×
a11
+
v2
×
a12
f(u2) =
v1
×
a21
+
v2
×
a22
g(v1) =
w1
×
b11
+
w2
×
b12
g(v2) =
w1
×
b21
+
w2
×
b22
|
そこで,
g(f(u1))
=g(
v1
×
a11
+
v2
×
a12
)
=
g(v1)
×
a11
+
g(v2)
×
a12
=
(
w1
×
b11
+
w2
×
b12
)
×
a11
+
(
w1
×
b21
+
w2
×
b22
)
×
a12
=
(
w1
×
b11
×
a11
+
w2
×
b12
×
a11
)
+
(
w1
×
b21
×
a12
+
w2
×
b22
×
a12
)
=
w1
×
(
a11
×
b11
+
a12
×
b21
)
+
w2
(
×
a11
×
b12
+
a12
×
b22
)
g(f(u2)) =
=g(
v1
×
a21
+
v2
×
a22
)
=g(v1)
×
a21
+
g(v2)
×
a22
)
=
(
w1
×
b11
+
w2
×
b12
)
×
a21
+
(
w1
×
b21
+
w2
×
b22
)
×
a22
)
=
(
w1
×
b11
×
a21
+
w2
×
b12
×
a21
)
+
(
w1
×
b21
×
a22
+
w2
×
b22
×
a22
)
=
w1
×
(
a21
×
b11
+
a22
×
b21
)
+
w2
×
(
a21
×
b12
+
a22
×
b22
)
|
一方
g(f(u1))
=
w1
×
c11
+
w2
×
c12
g(f(u2))
=
w1
×
c21
+
w2
×
c22
|
よって,
c11
=
a11
×
b11
+
a12
×
b21
c12
=
a11
×
b12
+
a12
×
b22
c21
=
a21
×
b11
+
a22
×
b21
c21
=
a21
×
b12
+
a22
×
b22
|
そこで,fとgの合成に対応する行列の計算を,つぎのように定めればよいことになる:
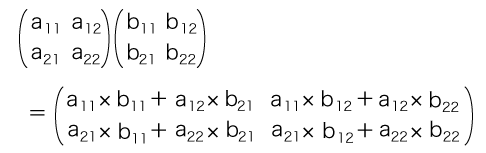
|