
この線型変換 f は,枠 { (1, 0), (0,1) } をつぎのように変換する:
| (1, 0) | → | (1.5, -0.7) |
| (0, 1) | → | (-0.6, 0.9) |
そしてこれに伴って,x = m,y = n ( m, n = 0, ±1, ±2, ‥‥) の格子がつぎのように赤色の格子へと歪む:
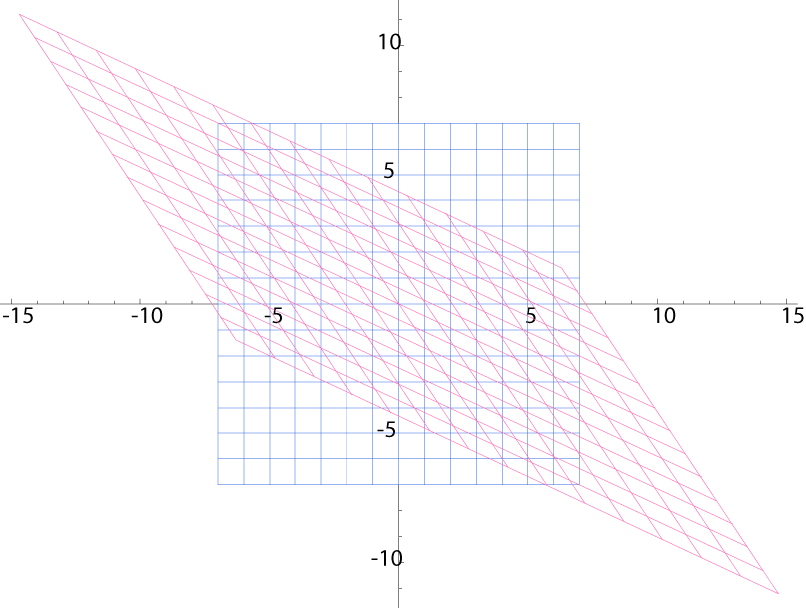
ここで,もとの格子の各交点がどこに移動するかを,矢線で表してみる:
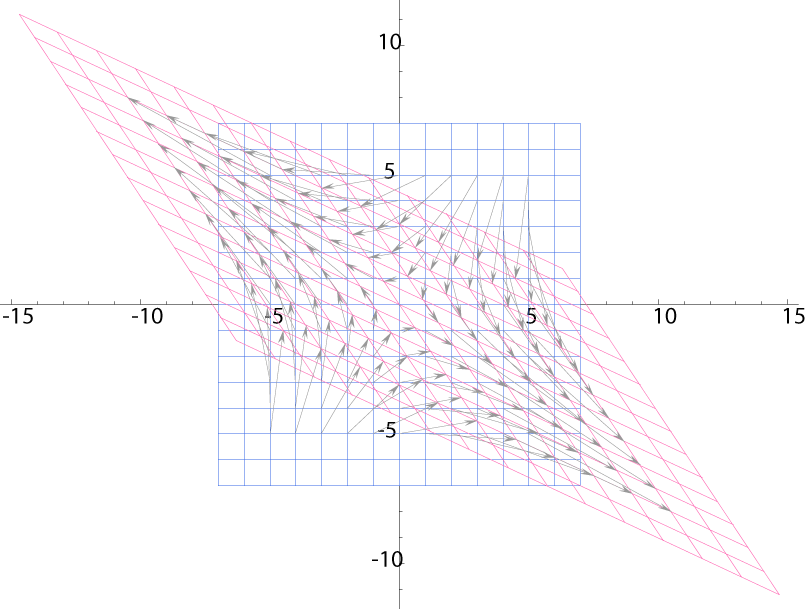
さて,この矢線図をじっと見てみる。
本来存在していない何かが見えてくるだろう:
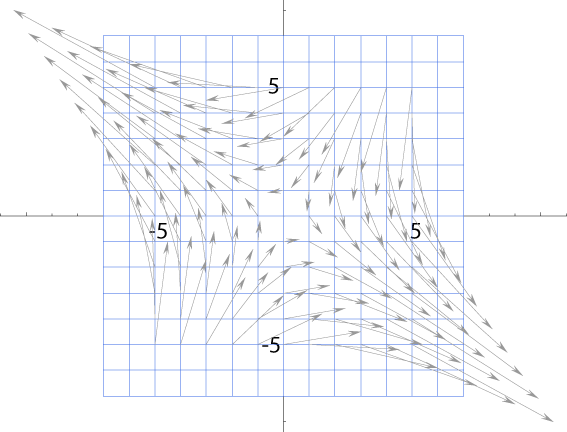
見えてきたものを確認しよう (下のアイコンをクリック):


この軸の意味は何だろう?
──つぎが,この軸の意味である:
「軸と同方向のベクトルに対しては,線型変換 f が単純に倍変換になっている」
計算によって,つぎの二つを同時に求めることができる:
- 2本の軸の式──あるいは,軸と同方向のベクトル (「固有ベクトル」と呼ぶ)
- 各軸の上で f は倍変換になっているが,この倍の値 (「固有値」と呼ぶ)
計算方法は,つぎのようになる:
f は,求める軸の上のベクトル (x, y) に対しては倍変換になっている。
k 倍であるとしよう。
f の表現行列を A とすると,つぎのようになっているということである:
これを計算すると,
(1.5x + (-0.6)y,(-0.7)x + 0.9y) = (kx,ky)
⇒ (1.5 - k) x + (-0.6)y = 0,(-0.7) x + (0.9 - k) y = 0
⇒ (1.5 - k) (0.9 - k) x ー (-0.7) (-0.6) x = 0
⇒ (1.5 - k) (0.9 - k) ー (-0.7) (-0.6) = 0
⇒ k2 - 2.4 k + 0.93 = 0
⇒ k = (12 ± √51)/10
⇒ k ≒ 0.5,k ≒ 1.9
上に出てきた関係式
(1.5 - k) x + (-0.6) y = 0
に k = 0.5 を代入すると,
(1.5 - 0.5) x + (-0.6) y = 0
⇒ y = 5/3 x
また,k = 1.9 を代入すると,
(1.5 - 1.9) x + (-0.6) y = 0
⇒ y = -2/3 x
ということで,2本の軸の式と各軸に対する固有値が,求まった。
以上のことから,つぎのことが導かれる:
この軸を最初から座標軸として選んでいたら,f はつぎの枠変換になっている:
| (1, 0) | → | (0.5, 0 ) |
| (0, 1) | → | ( 0, 1.9) |
そしてこれに伴い,次の図で青の平行四辺形が緑の平行四辺形に歪むように,全体が変形:
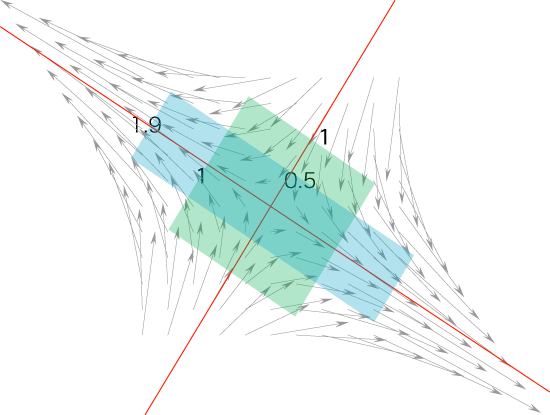
特に,線型変換 f を表現する行列が簡単な形 (「対角行列」)になる。

これは,小学算数でやったつぎのことと対応している:
「単位の取り直しによって,量の測定値を簡単にする」
|