一般に,ベクトルにおいては,(1) ベクトルに対するスカラ(数) の倍作用と,(2) ベクトルの和が,つぎのように定義されています:
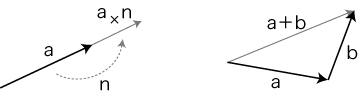
2次元実ベクトルでは,これの「倍と回転」が複素数の「倍作用」になりました。そして,複素数と2次元ベクトルが,「数と量」の関係になりました。 ( 複素数倍 ) 複素数倍 )
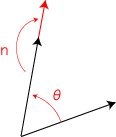
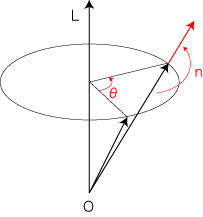
3次元実ベクトルの場合,「回転」は「一つの有向直線を回転軸とする回転」ということになります。
回転方向は,有向直線の向きと対面したときの左回り (時計の反対回り) を正と決めます。(言い換えると,回転して右ネジが進む方向と有向直線の向きが一致するときが,正。)
3次元実ベクトルに対する「回転・倍」の作用:
|
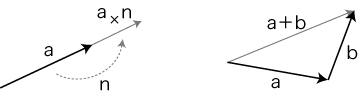
 複素数倍 )
複素数倍 )


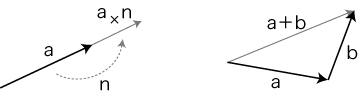
 複素数倍 )
複素数倍 )

