v を (1, 0) とするように x-y 座標をとる。 f は,f(v) = ( ax, ay ) で決まる。 「一つのベクトルの移動先が決まれば,すべてのベクトルの移動先が決まる」ということです。 (これは,「作用」が「数」に昇格するための基本要件です。) ここで,「v を (1, 0) とするように x-y 座標をとる」に注意しましょう。 「任意のベクトル v に対し,これを (1, 0 ) とする x-y 座標」が一意に決まらないと,「f は,f(v) = ( ax, ay ) で決まる」のようにできません。 x 軸は一意に決まります。 y 軸はどうでしょう? 黒板に,x軸を任意の傾きで書きます。 すると,このx軸に対してy軸が決まります。 すなわち,原点を中心にして,x軸を時計の針と反対回り (左回り) に 90゜回転したのが,y 軸になります。 この操作は,3次元に棲むことで可能になっています! 2次元に棲んでいたら,x軸に対する y 軸を決めることができません。 どういうこと? 「時計の針と反対回り (左回り)」は,黒板に正対するポジションをとることで言えることです。 このポジジョンは,黒板の「前と後ろ (表と裏)」を定めることのできるポジションです。 2次元の中に棲む者は,「前と後ろ (表と裏)」を定めることができません。 以上のことを,もう少し数学的な表現を使って,まとめましょう。 2次元ベクトル空間の変換としての「回転・倍」は,つぎのように3次元で考えています: 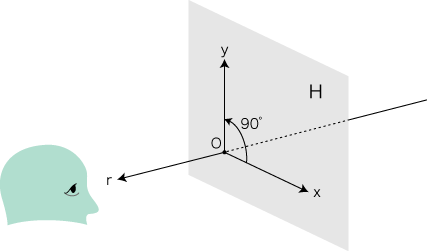
<埋め込み>を数値的に扱えるように,別の言い方も示しておきます: 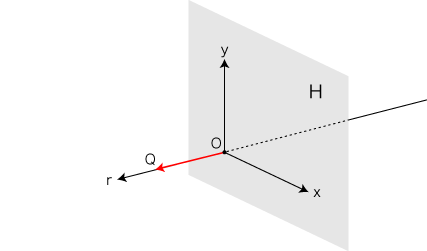
|
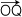 で考えるとき,
で考えるとき,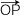 = 0 となるベクトル
= 0 となるベクトル