「角度 (角の大きさ)」は,「回転の大きさ」のことばを使って定義されることになります。 この「回転の大きさ」を扱うためには,その前に「回転」の意味が定まっていなければなりません。 すなわち,何に対して何をすることを「回転」というのか?ということです。 ユークリッド空間の幾何学は,「回転」を,最終的につぎの形に還元します。
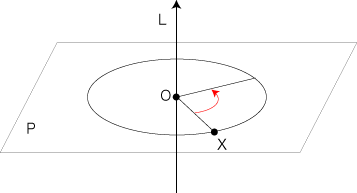 Xの回転は,Lに「正の方向」を定めていることにより,「右回りどれだけ」「左回りどれだけ」で表現されます。 ここで「超平面」ということばが出てきました。 これについて簡単に説明します。 3次元空間では,「空間」「平面」「直線」「点」があります。 2次元空間だと,「平面」「直線」「点」になります。 この調子を4次元でもやると,「全空間」「空間」「平面」「直線」「点」の5つになります。 5次元だと,「全空間」「4次元の空間」「空間」「平面」「直線」「点」の6つです。 この6つの表現に一貫性/連続性がないのは,3次元空間 (わたしたちが「リアルな空間」ということにしているもの) で使っている「空間」「平面」「直線」「点」のことばに縛られているからです。 そこで,「超平面」ということばを使うことにします。 すなわち,リアルな空間として3次元空間で使ってきた「空間」「平面」「直線」「点」を,それぞれ「3次元の超平面」「2次元の超平面」「1次元の超平面」「0次元の超平面」と呼ぶようにします。 上の「回転」の定義に戻ると,
Sが3次元 (「空間」) だったら,Pは「平面」 Sが4次元だったら,Pは「空間」 ここで,「アレ?!」と思いませんでしたか。 「平面Sでの,Oを回転の中心とする,P上の,Xの回転」とは,何でしょう? 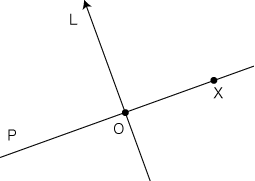 これは,「Oを中心とするP上の対称点に移るか,そのままでいるか」の2通りの操作ということになります。 これが,「平面」における「回転」です。 このように言うと,つぎの反論がきっと出てくるでしょう:
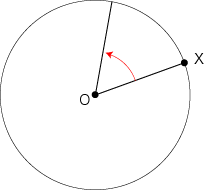 しかし,この絵を見ているあなたの眼は,どこにありますか? 3次元空間の中にありますね。 上の回転を考えているときは,暗黙に3次元空間を使っています。 そして,Oを通って自分の眼Eに向かう有向直線を,暗黙に回転軸として使っているのです。
あなたは,右回り(反時計回り) を決められませんから,指示された操作をすることができません。
|