6.2.2 “１と見る”
量の系 ((Ｑ,＋),(Ｎ,＋,×),×) の単位ｕからは，“単位ｕによる測定”を意味する関数
ｕ：Ｑ─→Ｎ； ｕ×ξ 
ξ（ξ∈Ｎ）
(§8.1.1）が導かれ，さらに量としての数との同型
(ｕ,id)：((Ｑ,＋),(Ｎ1,＋,×),×) ─→ ((ＮQ,＋),(Ｎ2,＋,×),×)
（Ｎ1＝Ｎ2＝ＮQ＝Ｎ）
が導かれる。そしてこの同型において，Ｑの要素ｘ＝ｕ×ξ（ξ∈Ｎ1）は１×ξ＝ξ（左辺のξはＮ2の要素，右辺のξはＮQの要素）と対応する。
小学校算数では伝統的に“割合”指導の一環として“１と見る”が主題化されているが，以上述べたことが
“ｕを１と見たとき，ｘはξ”
の言い回しの意味である。現行で指導されている形に引き寄せてこれを図式化すれば，
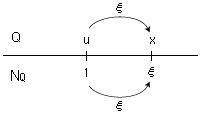
のようになる。特に,“１と見る”の主題化では，“量としての数”が暗黙に導入されていることになる。
しかしこれは，いまの数指導の駄目な局面の一つである。学習者には何よりも先ず，量と数の区別──図式的には，両者がノードとリンクの関係にあること（上図のＱの段）──が確実に指導されねばならない。しかし“１と見る”の指導はこの見方を壊すことの方に向いている。
本来なら，《数と量をしっかり区別するよう指導した上で“量としての数”という見方も指導する》という具合になるわけである。数と量の混同は，数と量の区別の上にはじめて可能になる高等技術である。
しかも，この高等技術は不可欠な主題というわけでもない。実際,“ｕを１と見る”では単に“ｕを単位とする”でよいわけである。