複素数を平面上に配置することができます。
すなわち,つぎのような対応をつくることができます:
「任意の数に対し,それに対応する平面上の一点が決まる。」
方法は,つぎのようになります:
- 平面上の任意の一点を,「基準」としてとる:

- 平面上に有向線分を任意の長さ任意の方向で書き,「単位」とする:

- (−1)+(+2)i に対応する点を求めるとしよう。
単位の (−1)+(+2)i 倍の有向線分を,つぎのように置く:
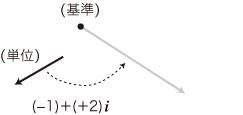
- そして,これの先端にある点を, (−1)+(+2)i に対応する点とする:
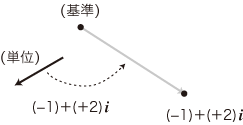
- 基準の点と対応する数はあるか?
a+bi のa,bを0に近づけると,対応する点は基準の点に近づく。
よって,0に基準の点が対応している:

|