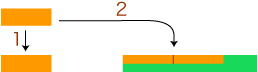
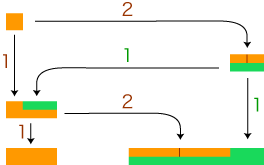
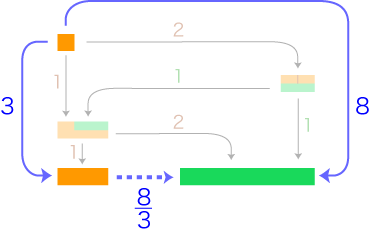
このときの比 (倍関係) の表現のきまりはつぎのようになります:
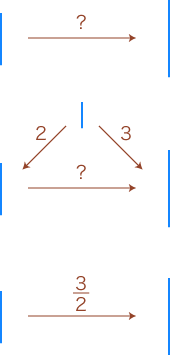 小学校では「3/2」を「2つに分けた3つ」と読ませていますが,これは「左辺の量を2つに分けた3つが右辺の量」から来ているわけです。 つぎが,ここでの比表現の要点になります:
参考:ユークリッドの互除法 分数倍の値は,試行錯誤的に物を操作して求めるしかないように,一見思われます。しかしそうではありません。分数の値を求める手順があります。言い換えると,分数を値とするきちんとした測定法があります。 ──以下がそれです: この手順 ( 余り同士の互除を,余りがなくなるまで続ける) は,ユークリッドの互除法と呼ばれています。 ユークリッドの互除法を使うと,つぎの両方が同時に得られます: |