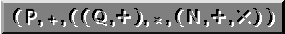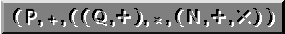ここまでの学習を終えて,わたしたちは「位・量・数」の形式:
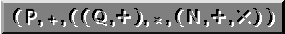
の理解に到達しています。
いまこの高見に立ったところで,「位・量・数」の形式を改めて構築してみましょう。
ステップ1
- 量は,一つのシステム(体系)です。
- このシステムには,数が部品として組み込まれています。
- この数は,量の測定で「測定値」として使われるものです。
- ある量は自然数を組み込んでいます。ある量は実数を組み込んでいます。また,ある量は複素数を組み込んでいます。
- どのような数の系が部品になっているかで,量の様相ががらっと変わってきます。
- 例えば,あるもの・ことの「個数」は,自然数を部品とした量です。「温度(の昇降)」は,「正負の数」(整数あるいは有理数あるいは実数)を部品とした量です。
- というわけで,量を(Q,N)のように表現することにします。Qは量,Nは測定値に使われる数の系です。
- 例えば,(りんごの個数,自然数),(長さ,正の実数),(温度,整数)といった具合です。
- 注意:(温度,整数)のような組み合わせですが,これは絶対的/論理的なものではありません。用途に応じて(温度,自然数)であったり(温度,実数)であったりするでしょう。それは,わたしたちがその都度(明示的あるいは暗黙的に)決めていることです。
- (Q,N)でのQ,Nは,集合です。
- (長さ,正の実数)を例にしましょう。
いろいろな長さがありますが,これら長さ全体の集合が,(長さ,正の実数)の「長さ」です。(もちろん,こんなものはフィクションですが。)
「正の実数」は,正の実数全体の集合です。
ステップ2
- Qの要素とNの要素は,「測定」という関係でつながっています。
- 「測定」とは,Qの要素qに対して,「qはuのn倍」という表現をつくる行為のことです。
ここで,uは,「単位」という呼び名で特別視されているQの一つの要素。そしてnはNの要素です。
ちなみに,この表現の中のnは「測定値」と呼ばれます。
- 一般に,Qの要素qとNの要素nに対する「qのn倍」を,「倍」の記号「×」を導入して,「q×n」と書くことにしましょう。
- というわけで,システム(Q,N)には「倍作用 ×」が部品として組み込まれていることになります。
これを明示するために,(Q,N)を新たに(Q,×,N)と書くことにしましょう。
ステップ3
- Qには,部品として加法があります。実際,Qの二つの要素q,rに対してはそれの和が考えられています。
- Qの要素q,r対する「qとrの和」を,「和」の記号「+」を導入して,「q+r」と書くことにしましょう。
- Qに加法があることを明示するために,(Q,×,N)を新たに((Q,+),×,N)と書くことにしましょう。
ステップ4
- Nには,部品として加法と乗法があります。実際,Nの二つの要素m,nに対してはそれの和と積が考えられています。
- Nの要素m,n対する「mとnの和」を,「和」の記号「+」を導入して,「m+n」と書くことにしましょう。
また,「mとnの積」を,「積」の記号「×」を導入して,「m×n」と書くことにしましょう。
- Nに加法と乗法があることを明示するために,((Q,+),×,N)を新たに((Q,+),×,(N,+,×))と書くことにしましょう。
ここまで
以上のステップを踏んで,わたしたちは「量」のつぎの表現に到達しました:
( (Q,+), ×, (N,+,×))
ステップ5
- 位は,一つのシステム(体系)です。
- このシステムには,量が部品として組み込まれています。
- この量は,位を表現するときに「基準からの隔たり」として使われるものです。
- 例えば,「時刻」は,「量」としての「経過時間」を部品とした「位」です。
「高さ」は,「量」としての「上下移動」を部品とした「位」です。
- というわけで,位を(P,Q)のように表現することにします。Pは位,Qは「基準からの隔たり」の表現に使われる量です。
- 例えば,(時刻,経過時間),(高さ,上下移動)といった具合です。
- Pは,集合です。
- (時刻,経過時間)を例にしましょう。
いろいろな時刻がありますが,これら時刻全体の集合が,(時刻,経過時間)の「時刻」です。(もちろん,こんなものはフィクションですが。)
ステップ6
- Pの要素とQの要素は,「ずらし」という関係でつながっています。
- 「位を定める」とは,Pの要素Pに対して,「Pは位Oからqだけずれている」という表現をつくる行為のことです。
ここで,Oは,「基準」という呼び名で特別視されているPの一つの要素。そしてqはQの要素です。
- 一般に,Pの要素XとQの要素xに対する「Xからxだけずれた位置」を,「ずらし」の記号「+」を導入して,「X+x」と書くことにしましょう。
- というわけで,システム(P,Q)には「ずらし作用 +」が部品として組み込まれていることになります。
これを明示するために,(P,Q)を新たに(P,+,Q)と書くことにしましょう。
ラスト
(P,+,Q)のQは,( (Q,+), ×, (N,+,×))のようになっていました。したがって,「位」(形式)はつぎのようになります:
(P,+, ( (Q,+), ×, (N,+,×) ) )