(
P,
+,
(
Q,
+
),
x,
(
N,
+,
x
)
)
の中の P, Qを N に,作用の +, x をそれぞれNの加法 + と 乗法 x に,Qの加法の + をNの加法 + に,置き換えて得られる
(
N,
+,
(
N,
+
),
x,
(
N,
+,
x
)
)
は,「数」を「位・量・数」と見る見方になります。── 特に,
(
(
N,
+
),
x,
(
N,
+,
x
)
)
は,「数」を「量」と見る見方になります。
- このように言えばたいへんな内容に思われるかも知れませんが,この内容は小学算数の中にあります。「数直線」がそれです。
数直線に目盛られている数は,「位」としての数です。
- 大学数学の「線型代数」では,
「線型空間のスカラー体Kに対し,Kを線型空間と解釈する方法」
が学習の早い段階で主題になりますが,やっていることは,ここで示した「数を量と見る」と同じです。
- 「「位・量・数」としての数」(数に対する「位」「量」の解釈)を,絵にしてみましょう:
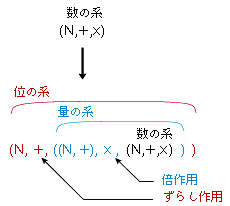
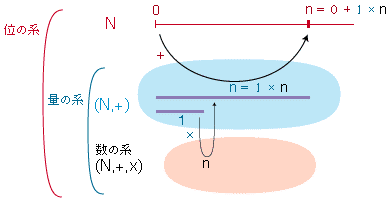
- 「位」「量」はリアルに存在しているのではなく,わたしたちの解釈として「存在」しています。
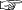 「フィクションとしての「量」」
「フィクションとしての「量」」
そして,リアルに対して「位」「量」を抽象をするときに,「「位・量・数」としての数」が形として(暗黙に)使われています。
- 実際,つぎの形式が「位・量・数」です。「「位・量・数」としての数」と同型であることを確認して下さい。
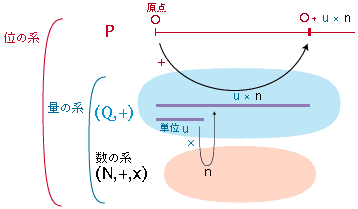
ちなみに,同型対応(「コピーのきまり」)はつぎのようになります:
- 第2項の
(Q, +)
と
(N, +)
の間では,
uxn
←→
n
- 第1項の
P
と
N
の間では,
O+uxn
←→
n




 「フィクションとしての「量」」
「フィクションとしての「量」」
