「位・量・数」は,じつは形(形式)です。
形式自体は単純です(もっとも,単純なのは,微妙な問題にすべて目をつぶった結果だとも言えますが)。
しかし,この形式の理解は簡単ではありません。辛抱強く理解に努めて下さい。
ゴールはつぎの形式です:
(
P
,
+
,
(
Q
,
+
)
,
x
,
(
N,
+
,
x
)
)
- 数の使用においては,「位」,「量」,「数」という3つの異なる存在が現れています。そこで,「位」の集合P,「量」の集合Q,「数」の集合Nを考える(想像する)ことにします。
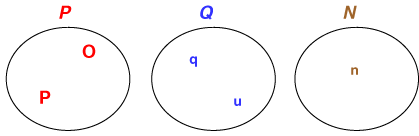
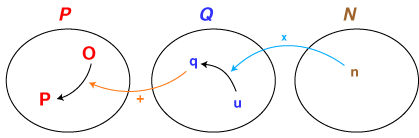
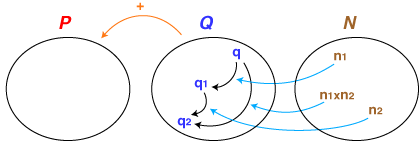
- 集合P,Q,Nは「作用」という関係でつながっています。すなわち,
- Pの要素に対しQの要素は「ずらし」の作用をする
- Qの要素に対しNの要素は「倍」の作用をする
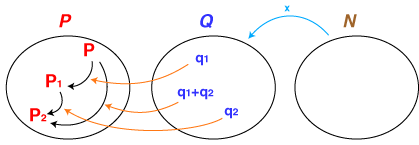
- 移動a,bの和,経過時間a,bの和,‥‥ というように,わたしたちは集合Qの中では加法を考えています。
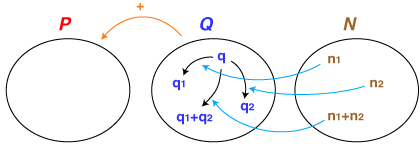
- 2倍と3倍の和は(2+3)倍,2倍して3倍すると(2×3)倍,‥‥ というように,わたしたちは集合Nの中では加法と乗法を考えています。
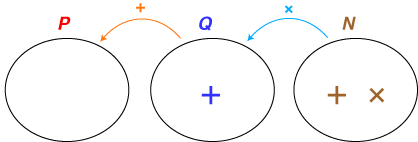
- 結局,「位・量・数」の形式化として,つぎのものが得られました:
(
P
,
+
,
(
Q
,
+
)
,
x
,
(
N,
+
,
x
)
)
ここで,「数」は,自然数,有理数,実数などから,ケース・バイ・ケースで選ばれます。






