これは,位の形式をもつ。 実際,Nを数の系として伴う位は,「(N,+,((N,+),×,(N,+,×))) に同型な系」として,定義されることになる。 ──「数」の以前に「位」が存るのではない。「数」をもちいて「位」がつくり出されるのである。 位の形式を表すものとしてのこの (N,+,((N,+),×,(N,+,×))) は,<位の普遍対象>ということになる。 このように理解したところで,系 (N,+,((N,+),×,(N,+,×))) そのもの,あるいはこの系の左端のNの要素を,「位としての数」と呼ぶことができる。 (N,+,((N,+),×,(N,+,×))) における数の3態 (数・量・位) は,つぎの模式図に表される: 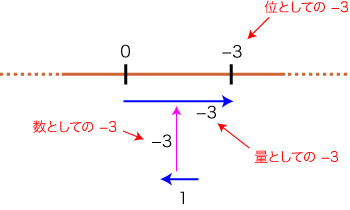
さて,この「位としての数」「位の普遍対象」の概念は,そのまま「座標空間」「アフィン空間の普遍対象」の概念に一般化される。 ──「一般化」の意味は,「次元拡張」である。 「アフィン空間の普遍対象」は,線型代数での主題の一つになるものである。 「Nをスカラの系として伴うn次元アフィン空間」の普遍対象として,(Nn,+,((Nn,+),×,(N,+,×))) が (明示的あるいは非明示的に) 登場する。 よく注意されたい。 ちなみに,「数直線」は,直線上に<位としての数>を置いていることになる。 ──実際,<位としての数>を置く手順の上で,<量としての数>と<数としての数>が上の図のように現れる。 |