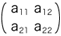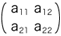- 比例関係
2量 D, D' の間の比例関係 f : D → D' は,つぎの条件で定義されます:
f( x × n) = f( x ) × n
(「一方が 2倍, 3倍, ‥‥ になればもう一方も 2倍, 3倍, ‥‥ になる」)
いま,D, D' の単位をそれぞれ決めます── u と v とします。
このとき, u に対する値が n の x に対し,v に対する f( x ) の値は,つぎのようになります:
n × a
f( u ) = v × a
f( u × n ) = f( u ) × n= ( v × a ) × n= v × (n × a)
- 線型写像
2量の比例関係は,「2次元の実ベクトル空間 D, D' の間の線型写像 f : D → D'」の概念に拡張されます。
この「拡張」の内容は,つぎの条件です:
f( x × n) = f( x ) × n
f( x + y) = f( x ) + f( y )
いま,D と D' の基底をそれぞれ決めます── { u1, u2 } と { v1, v2 } とします。
このとき,{ u1, u2 } に対する値が
( n1, n2)
の x に対し,{ v1, v2 } に対する f( x ) の値は,つぎのようになります:
(
n1 × a11 + n2 × a21,
n1 × a12 + n2 × a22,
)
ここで,a11, a12, a21, a21, は,つぎの関係から出てくる数です:
f( u1 )
= v1 × a11 + v2 × a12
f( u2 )
= v1 × a21 + v2 × a22
f( u1 × n1 + u2 × n2 )
= f( u1 ) × n1 + f( u2 ) × n2
= ( v1 × a11 + v2 × a12 ) × n1 +
(v1 × a21 + v2 × a22 ) × n2
= v1 × (n1 × a11 + n2 × a21)
+ v2 ( n1 × a12 + n2 × a22 )
|
| 比例関係 |
線型写像 |
| f( u ) = v × a |
f( u1 )
= v1 × a11 + v2 × a12
f( u2 )
= v1 × a21 + v2 × a22
|
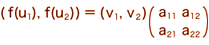
|
|
|
値 ( n1, n2) に
値
(n1 × a11 + n2 × a21, n1 × a12 + n2 × a22 )
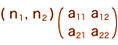 が対応
が対応
|
|
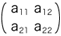
|