さて，この一般化において，「比例関係」はどうなるでしょう？ 比例関係は，二つの量の系（例えば，時間と距離）をまたがる関係です。 そしてこれは，対応する量の組を一つ確定すれば，すべての対応が決定してしまう関係でした。 ──例えば，速さは「秒速5m」のように表現されますが，これは時間と距離の対応を一つ (「秒には5m」) 示せば十分だという事実を使っているわけです。 この比例関係の一般化は，「線型写像」になります。 以下，このことを説明します。 比例関係は，「一方が２倍，３倍，････になるとき，もう一方も２倍，３倍，････になる」という関係です。 関数としては，Kが実数体  あるいは有理数体 であるときの１次元線型空間（D,K),(D',K）に対する関数 f : D ─→ D' というふうになります。
そして，「一方が２倍，３倍，････になるとき，もう一方も２倍，３倍，････になる」の条件は，つぎの式に表現されます：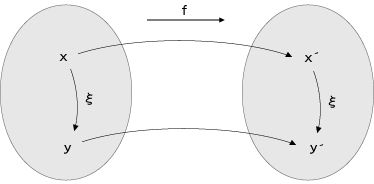 
「単位」は「基底」の概念へと拡張されます。よって，《単位の写る先がわかれば全ての要素の写る先がわかる》は，つぎのものになります：
この条件の追加は，比例関数の自然な拡張を損なうものではありません。 実際，比例関数の場合, 「f(ｘ＋ｙ)＝f(ｘ)＋f(ｙ)」 は「f(ｘ×ａ)＝f(ｘ)×ａ」の含意になっています：
こうして,「比例関数」の拡張は，条件： f(ｘ＋ｙ)＝f(ｘ)＋f(ｙ)
|