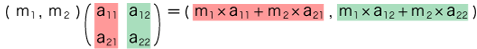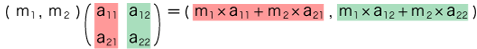- 「単位を変えると測定値が変わる」には,「基底を変えるとベクトルの表現が変わる」が対応します。基底の変更は「基底変換」と呼ばれます。
- 単位変更の計算
単位uに対する量xの値が3であるとします。そして,u = v ×2 の関係にある単位vを新たにとります。さて,単位vに対する量xの値は?
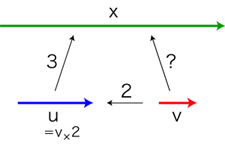
x
= u ×3
= (v × 2) ×3
= v × (2 × 3)
= v × (3 × 2)
|
- 基底変換の計算
基底 (u1, u2) に対するベクトルxの値が (2, 1.5) であるとします。そして,
u1
= v1 × 1
+ v2 ×(−1)
u2
= v1 × 2
+ v2 × 1
|
の関係にある基底 (v1, v2) を新たにとります。さて,基底 (v1, v2) に対するベクトルxの値は?
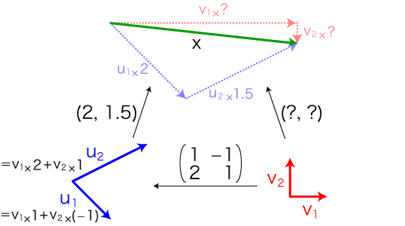
x
= u1 × 2
+ u2 × 1.5
= (v1 × 1
+ v2 × (−1))
× 2
+ (v1 × 2
+ v2 × 1)
× 1.5
= v1 × (1×2)
+ v2 × ((−1)×2)
+ v1 × (2×1.5)
+ v2 × (1×1.5)
= v1 × (1×2 + 2×1.5)
+ v2 × ((−1)×2 + 1×1.5)
= v1 × (2×1 + 1.5×2)
+ v2 × (2×(−1) + 1.5×1)
|
- 単位変更の計算
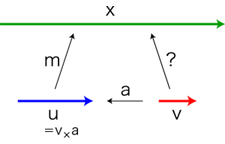 x
= u ×m
= v × ?
x
= u ×m
= v × ?
u
= v ×a
m ×a = ?
- 基底変換の計算
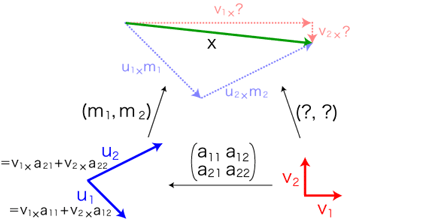
二つの基底 (u1, u2),(v1, v2) に対し
x
= u1 × m1
+ u2 × m2
= v1 × ?1
+ v2 × ?2
u1
= v1 × a11
+ v2 × a12
u2
= v1 × a21
+ v2 × a22
|
| (*) |
m1 × a11
+ m2 × a21
= ?1
m1 × a12
+ m2 × a22
= ?2
|
|
- 特に,基底変換による新しいベクトル表現は,旧基底のベクトルを新基底で表現したときの値で決まってしまいます。すなわち,
と計算式 (*) で決まります。
またこれより,上の4つの数の組 (「行列」) が単位換算のときの a に対応していることが,見てとれます。
- また,新基底に対するベクトル値を求める筆算形式が,つぎのように編み出されます:
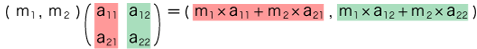
|