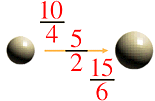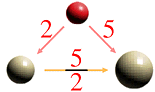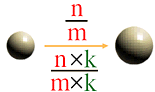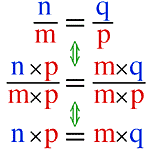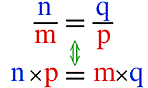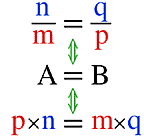 Shockwave 640x480 (36K) Shockwave 640x480 (36K)
For each rational relation there exist infinite number of pairs of natural numbers that represent it.
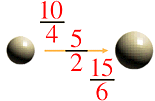
There exist a rule in this set of pairs.
Let's recall this rule.
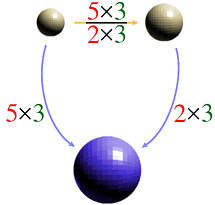
This is the structure of the ration "5/2".
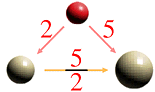
Here, consider the quantity 3 of which is equal to the quantity colored red.
Then we have this picture of structure.
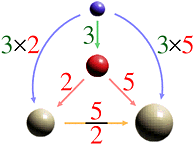
If we measure the ratio of the original two quantities by the quantity colored blue, the ratio becomes expressed as "(3x5)/(3x2)" .
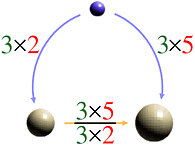
Now, how does the story become if we use the "common multiple" instead of the "common divisor"?
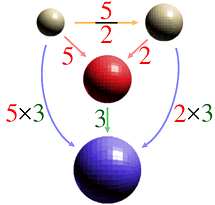
Summing up:
In general, these two expressions are equivalent.
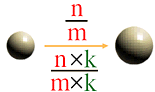
Now let's see what relation holds between four natural numbers m,n,p,q in this equality.
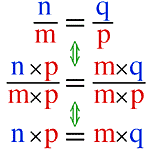
Finally, this relation holds.
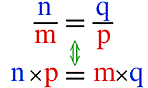
Let's check this fact on pictures.
Firstly, let us understand that the following relation of multiples holds.
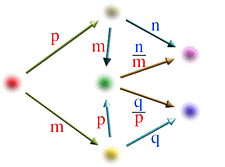
This includes the following:
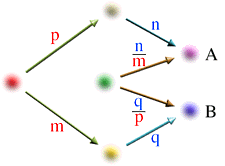
And from this diagram we can read the following equivalent relation.
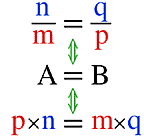
|
 Shockwave 640x480 (36K)
Shockwave 640x480 (36K)