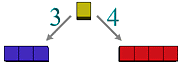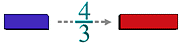 Shockwave 640x480 (29K) Shockwave 640x480 (29K)
Not depending on categories of numbers, the expression of a quantity using a number n is always of the form :
"n unit"
The idea of the "rational number" is to express a ratio, or a multiplier, as follows.
Given two quantities:

if there exists a common divisor to which those two quantities are in the ration of 3 and 4, respectively ....
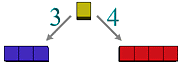
we represent the ratio between given two quantities , or the multiplier that transforms the first quantity to the second one, as "4/3".
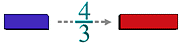
This way of definition of "3/4" is equivalent to the following.
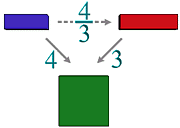
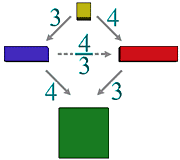
Let's remark the point.
The motive of the introduction of the rational number is to overcome a case where the expression "n simplex" using a natural number n does not work.
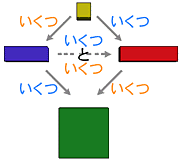
The idea of the rational number is very simple :
"if you cannot express an multiplier by using one nutural number, then try two."
|
 Shockwave 640x480 (29K)
Shockwave 640x480 (29K)