- 導入:√2 の実現
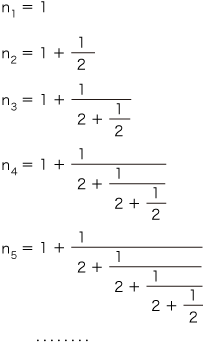
そして,この数列を √2 ということにしてしまいます。──実際には,√2 に近づく有理数列はいくらでも異なるとり方ができますから,そのような数列を一つに同一視するルール (「互いに限りなく接近するコーシー列」) を導入し,そうして一本化されたものを √2 とします。
- 「コーシー列」
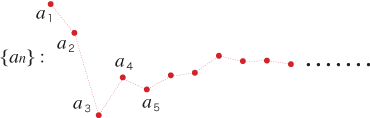
収束する数列は,先の方で項が互いに限りなく接近します。
また,√2 に近づく有理数列は,(有理数の世界では収束しませんが)「先の方で項が互いに限りなく接近」するものになっています。
この条件「先の方で項が互いに限りなく接近」に目をつけて,「コーシー列」の名を与えます。
「Cauchy 列」のイメージ
- 「互いに限りなく接近するコーシー列同士」
つぎに,互いに限りなく接近するコーシー列同士を,同じ仲間にします。
そして,同じ仲間のコーシー列全体を一つの実数と定めるというのが,実数構成のアイデアです。──その気持ちは:
互いに限りなく接近するコーシー列同士は,一つが収束すれば他も収束し,そしてその収束値も同じである。
しかし,有理数の世界で収束値を持てない場合もある。これが無理数を必要とする状況だ。
そこで,互いに限りなく接近するコーシー列の全体 (集合) を,一つの数(実数)ということにしてしまおう。
従来の有理数は,これに収束するコーシー列全体と同一視することで,実数になる。よって,この実数の構成は「有理数の拡張」を実現してしていることになる。
「互いに限りなく接近するコーシー列同士」のイメージ
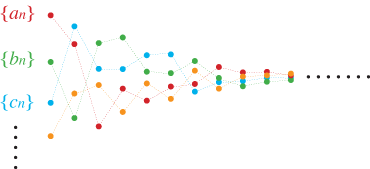
(互いに限りなく接近するコーシー列のグループを,
一つの実数ということにする!)
- 実数の和・籍
いま,コーシー列 {an} の属するクラスを [{an}] で表すことにして,実数の和と積をつぎのように定めます:
[{an}]+[{bn}]=
[{an+bn}],
[{an}]×[{bn}]=
[{an×bn}]
- さて,これで求めていた実数が得られたのでしょうか。
√2 に近づく有理数列{an} (例えば先の {n1, n2, ‥‥ } ) に対し,{an×an} は 2に収束します。よって,
[{an}]2 =[{an×an}] = 2
すなわち,x2 = 2 は実数では解をもつことになりました。
- 「これが実数 !?」と思われたかも知れませんが,ひじょうにテクニカルな装いになっているのは,他に依拠せず有理数のみから実数を構成しようとしているためです。
|

