有理数から実数を生み出す方法には,Cauchy列を用いるものと, Dedekind切断で実数を定義するものの,2つがある。 「既存の数の系から新しい数を生み出す」は,分数と整数を自然数から構築するところでもやっている。 そしてそのときには,構築の手順が存在した:
しかし,実数の構築の場合,Cauchy列の方法でも Dedekind切断の方法でも,有理数から実数をつくる手順は与えられない。 したがって,実数のこれらの導入には,何か<だまし>のようなものをどうしても感じることになる。 しかし,この<だまし>も,数学のうちである。 以下,Dedekind切断のアイデアを述べる。 「有理数から実数を生み出す」をやるわけであるが,結果先取りで,実数直線を考える。 そして,この直線を包丁で真っ二つに切断することを考える。 この切断は,刃先が有理数にあたるものと,無理数にあたるものの,二通りになる。 実際には,無理数はいまから構築するのであって,無理数はまだ存在しない。 そこで,実数直線から無理数を除いて,有理数だけにする。 すると先の切断は,刃先が有理数にあたるものと,刃先が何にもあたらないものの,二通りになる。 前者を「コツン(とあたる)」タイプ,後者を「スルー(と抜ける)」タイプと,呼ぶことにしよう。 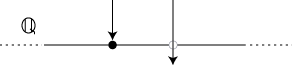
このとき,コツンタイプをこれまでの有理数と同一視し,スルータイプを「無理数」と定める。 そして,両者合わさって「実数」となる。 コツンタイプは,あたった有理数nを用いて, 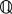 の二分割 { ]←, n], ]n, →[ } あるいは { ]←, n[, [n, →[ } で表すことができる。 の二分割 { ]←, n], ]n, →[ } あるいは { ]←, n[, [n, →[ } で表すことができる。
しかし,スルータイプの方は, 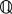 の二分割として記述する一般的形式は存在しない。無理数ごとに,個別に考えていくことになる。 の二分割として記述する一般的形式は存在しない。無理数ごとに,個別に考えていくことになる。
|
 ×
× √2 に対応する Dedekind 切断
√2 に対応する Dedekind 切断