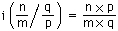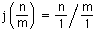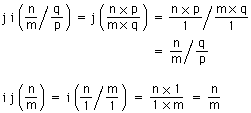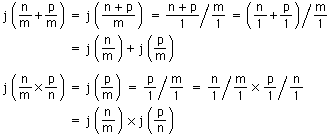4.3.2 (NR)RとNRの同型性
学校数学では,自然数m,n,p,qに対する ( R)R の要素 (n/m)/(q/p) と
R)R の要素 (n/m)/(q/p) と  R の要素 (n/m)×(q/p)-1(=(n×p)/(m×q))の同一視を暗黙に導入する(註1)。これは本来,“(NR)R とNR の同型”という主題になる。
R の要素 (n/m)×(q/p)-1(=(n×p)/(m×q))の同一視を暗黙に導入する(註1)。これは本来,“(NR)R とNR の同型”という主題になる。
実際,
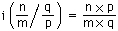
で定義される写像i:(NR)R ─→NR は,((NR)R,+,×)の(NR,+,×)の上への同型になっている。──これの逆同型は,
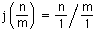
で定義される写像j:NR ─→(NR)R(註2)。
特に,(NR,+,×)からの((NR)R,+,×)の導出では,実質的に,新しい対象はつくられない。
(註1) 実際,“分数の分母や分子に分数が現われる数”のような発想(“繁分数")も現にある。この発想では,《“分数の分母や分子に分数が現われる”形態のものが何であり,かつ何故それが“数”と身分づけられるのか》という問いの立つことに気づかれていない。
(註2) (1) 先ず,jはiの逆写像:
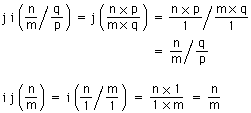
(2) さらに,j は準同形:
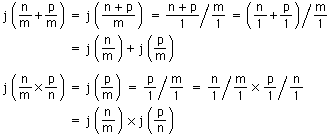
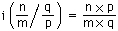
 R)R の要素 (n/m)/(q/p) と
R)R の要素 (n/m)/(q/p) と  R の要素 (n/m)×(q/p)-1(=(n×p)/(m×q))の同一視を暗黙に導入する(註1)。これは本来,“(NR)R とNR の同型”という主題になる。
R の要素 (n/m)×(q/p)-1(=(n×p)/(m×q))の同一視を暗黙に導入する(註1)。これは本来,“(NR)R とNR の同型”という主題になる。