5.3 有理数導出までの“数の拡張”方法
──比の系と差の系の導出
自然数以下の“数の構成”は，有理数がゴールの場合には，つぎの二つの生活実践的機能拡張の目的でなされる。一つは，量の自然数比の表現とそれを計算にのせることであり，そしてもう一つは，量の対称化の表現とそれを計算にのせることである。
この拡張は，自然数の系 (
,＋,×) から出発する“比の系と差の系の導出”になる。
そしてこの拡張は，
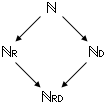
のように，RD（＝(R)D＝(D)R）が終点になって終わる(§4.3.4)。そして，R が分数の系（
で表わす)，D が整数の系
，RD が有理数の系
ということになる。
この意味で，整数と“分数”は，二つのパラレルな自然数拡張として，主題になる。