9.3.4 “量の積”の例


  1. 量の系（Ｑ,Ｎ）は，それ自身と“量としての数”(Ｎ,Ｎ）の積と見なせる：

    （Ｑ,Ｎ）（ＱＮ,Ｎ）

    実際，外算法×：Ｑ×Ｎ─→Ｑ は複比例関数。

  2. 量の系（Ｑ1,Ｎ)，(Ｑ2,Ｎ）に対し，（Ｑ2,Ｎ）は（Ｑ1,Ｎ）とＨom(Ｑ1,Ｑ2) の積と見なせる。

    （Ｑ1Ｈom(Ｑ1,Ｑ2),Ｎ）（Ｑ2,Ｎ）
    実際，関数：
    Ｑ1×Ｈom(Ｑ1,Ｑ2) ─→ Ｑ2；
    　　（ｘ,ｆ) ｆ(ｘ)　　　
    複比例関数。

  3. “長さ",“面積”をそれぞれ量の系（ＱL,+)，(ＱA,+）と見なすとき，ＱA はＱL とＱL の積と見なせる(“面積は長さと長さの積")。実際，長さの対 (ｘ,ｙ) に〈タテの長さｘ，ヨコの長さｙの長方形〉の面積を対応させる関数ｆ：

    ＱL×ＱL ─→ ＱA；
    は複比例関数。

  4. ＱL は，つぎの手続きのもとで，ＱL とＱL の積と見なせる(“長さは長さと長さの積")。
    　即ち，長さｕを一つ固定し，そして，与えられた長さｘ，ｙに対し長さｚをつぎのように定める：


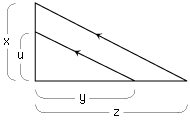
    このとき，関数ｆ：
    ＱL×ＱL─→ＱL；
    (ｘ,ｙ) ｚ
    は複比例関数である。