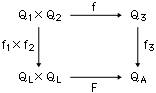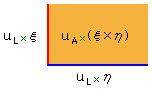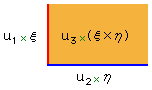9.3.5 量の積の“面積”図式
長さの系，面積の系をそれぞれ量の系
((ＱL,＋),(
+,＋,×),×)， ((ＱA,＋),(+,＋,×),×)
と見なす。長さの単位ｕLを定め，そして，一辺の長さがｕLの正方形の面積ｕAを，面積の単位と定める。
さらに，Ｆを，関係：
Ｆ(ｕL,ｕL)＝ｕA
で決まる複比例関数：ＱL×ＱL─→ＱA とする。長さｘ，ｙに対する面積Ｆ(ｘ,ｙ) は，タテの長さｘ，ヨコの長さｙの長方形の面積と一致する。
さて，一般に三つの量の系 ((Ｑi,＋),(+,＋,×),×) （i＝1,2,3）の間の複比例関数
ｆ：Ｑ1×Ｑ2 ─→ Ｑ3
は，以下の手続きによって，複比例関数Ｆと同一視できる。
即ち，Ｑiの単位ｕi（i＝1,2,3）を
ｆ(ｕ1,ｕ2)＝ｕ3
であるようにとり，
ｆi(ｕi)＝ｕL（i＝1,2），ｆ3(ｕ3)＝ｕA
で決まる同型
ｆi：Ｑi─→ＱL（i＝1,2）,ｆ3：Ｑ3─→ＱA
を介して，ｆとＦを図式：
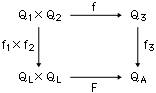
のように同一視する。
積ｆ(ｕ1×ξ,ｕ2×ξ) には面積Ｆ(ｕL×ξ,ｕL×η) ──即ち，タテの長さｕL×ξ，ヨコの長さｕL×ηの長方形の面積──が対応する。そこで，
ｆ(ｕ1×ξ,ｕ2×η)＝ｕ3×ζ
となるζを求めるためのξ×ηの計算が，長方形の面積計算のイメージで行なえることになる。
実際，面積図式：
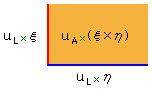
の中の単位を書き換えた
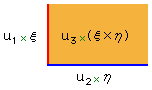
がｆの図式として使われるようになり，さらには，
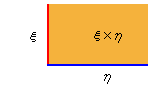
が，積ξ×ηの図式として使われるようになる。
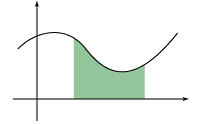
例えば積分計算(註)が面積計算の意識で行なえるのは，以上の理由による。
（註） 運動のグラフ表示で〈経過時間〉を横軸にとり〈速度〉を縦軸にとるとき,〈移動距離〉が面積の形で現われる：
