確率分布 P(X=n) に対し,これの「分散」──伝統的に V(X) と表記──を,つぎのように定義する:
V(X) = Σ{ (n ー E(X))2 × P(n) }
| 註: |
<2乗>は,「Σ{ (n ー E(X)) × P(n) } = 0」への対策。
|
| 例. |
サイコロの<nの目が出る>にnを対応させた確率分布
{ P(X=n) | n=1, 2, ‥‥‥, 6 )
の場合,「偏りのないサイコロ」では,
P(1) = ‥‥‥ = P(6) = 1/6, E(X) = 3.5
より,
V(X) = (1ー3.5)2 × 1/6 + (2ー3.5)2 × 1/6 + ‥‥‥ +(6ー3.5)2 × 1/6
=35/12
≒ 2.92
| |
確率分布 P(X=n) に対し,これの「標準偏差」──伝統的に σ(X) と表記──を,つぎのように定義する:
| 例. |
「偏りのないサイコロ」
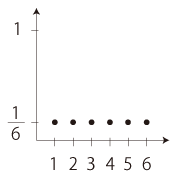
の場合 :
σ(X) = √ V(X)
= √ 2.92
≒ 1.71
「3, 4 に偏りのあるサイコロ」
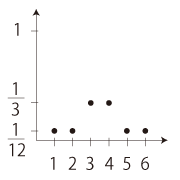
の場合 :
E(X) =1× 1/12 +2× 1/12 +3× 1/3
+4× 1/3 +5× 1/12 +6× 1/12
= 3.5
V(X) = (1ー3.5)2 × 1/12 + (2ー3.5)2 × 1/12 + (3ー3.5)2 × 1/3
+ (4ー3.5)2 × 1/3 +(5ー3.5)2 × 1/12 +(6ー3.5)2 × 1/12
≒ 1.58
σ(X) = √ V(X)
= √ 1.58
≒ 1.27
|
|