いま,半径rの球面を考える: 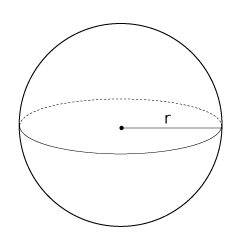
これの面積を,つぎの区分求積で考える: 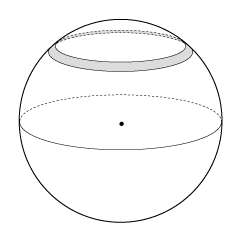
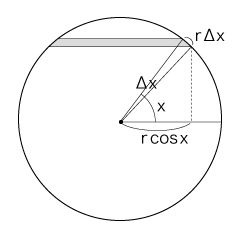
そこで,球の表面積は,つぎの積分で求められる: 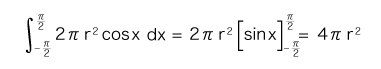
こうしてつぎの結論になる:
なお,スライスの面積の近似計算
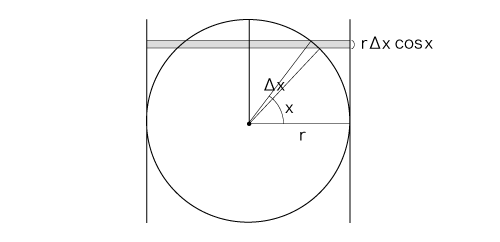
よって,球の表面積は,<底が半径rの円で高さが2rの円柱>の側面の面積と等しい。 そしてこの側面の面積を計算すると
|
| Up | 球の表面積 | 作成: 2013-01-25 更新: 2013-01-25 |
いま,半径rの球面を考える: 
これの面積を,つぎの区分求積で考える: 

そこで,球の表面積は,つぎの積分で求められる: 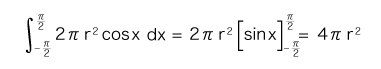
こうしてつぎの結論になる:
なお,スライスの面積の近似計算

よって,球の表面積は,<底が半径rの円で高さが2rの円柱>の側面の面積と等しい。 そしてこの側面の面積を計算すると
|