 (η1,・・・・,ηn);
(η1,・・・・,ηn);
ηi=ξ1×α1i+ ・・・・ +ξn×αni (i=1,・・・・,n)
| Up | English | 線型変換 |
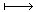 (η1,・・・・,ηn);
(η1,・・・・,ηn);
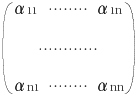
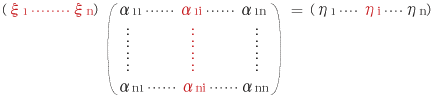
|
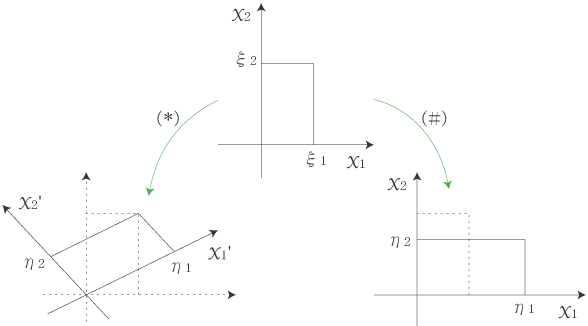
(*)《線型空間(D,K)の二つの基底{u1, ・・・・,un},{v1,・・・・,vn}に対し,
u1×ξ1+ ・・・・ +un×ξn =v1×η1+ ・・・・ +vn×ηn 》 |
|
(#)《線型空間(D,K)の基底{u1,・・・・,un}と線型変換(写像) f:D─→Dに対し,
f(u1×ξ1+ ・・・・ +un×ξn) =u1×η1+・・・+un×ηn 》 |