“現空間”の数学的定式化のここまでの段階──即ち,“現空間”を実アフィン空間(E,D,
 )として定式化している段階──では,二点に関する概念としては“一方の点に対する他方の点の変位(ベクトル)”が導入されています。
わたしたちは“二点X,Y間の距離”を“ベクトルXYの長さ”として定式化する(註1)。
)として定式化している段階──では,二点に関する概念としては“一方の点に対する他方の点の変位(ベクトル)”が導入されています。
わたしたちは“二点X,Y間の距離”を“ベクトルXYの長さ”として定式化する(註1)。
“ベクトルの長さ”の定義は,一定の条件を満たす関数
| Up | English | 二点間の距離とベクトルの長さ |
 )として定式化している段階──では,二点に関する概念としては“一方の点に対する他方の点の変位(ベクトル)”が導入されています。
わたしたちは“二点X,Y間の距離”を“ベクトルXYの長さ”として定式化する(註1)。
)として定式化している段階──では,二点に関する概念としては“一方の点に対する他方の点の変位(ベクトル)”が導入されています。
わたしたちは“二点X,Y間の距離”を“ベクトルXYの長さ”として定式化する(註1)。
 +
+
 +は≧0 である実数全体の集合)。──x
+は≧0 である実数全体の集合)。──x Dに対し,L(x)が“ベクトルxの長さ”と読まれる。なお,これの表記として |x| を用いることにします。
Dに対し,L(x)が“ベクトルxの長さ”と読まれる。なお,これの表記として |x| を用いることにします。
 x=0
x=0
 +
+
 X=Y
X=Y
| f: | (X,Y) 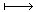 XY; XY;
E×E ─→ D |
| (註1) |
“二点間の距離”を“ベクトルの長さ”に帰着させて定義するここでのやり方は,あくまでも論理の上の処置(方便)です。
生活実践的には,点とベクトルの概念が相互依存的である(§3.2,(註1))のに対応して,二点間の距離とベクトルの長さの概念も相互依存的です。
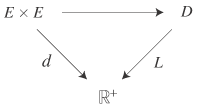
実際,L(x)は,X+x=YとなるX,Yに対するd(X,Y)のことです。
生活実践の上では,二点間の距離およびベクトルの長さは,所与ではなく人為です。 それは人の“測る”行為によって存在します。そして行為としての“二点間の距離を測る”と“一方の点に対する他方の点の変位(ベクトル)の長さを測る”の間には,区別が立たない。行為として両者を違えることはできない──あなたはできるか? |
| (註2) | この形式において“ベクトルの長さ”の概念を一般化したのが“ノルム”です。 ノルムとしてのL(x)の表記は ||x|| です。 |