 平均
平均
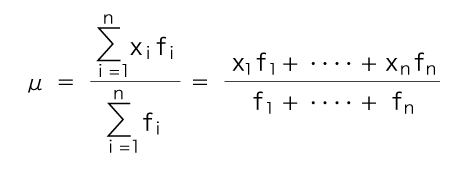
「相加平均」「加重平均」は,まったく別の概念である。 それぞれのイメージを,以下に示す:
「相加平均」と「加重平均」の本質的な意味の違いを見ないで,計算式で両者を区別しようとすると,つぎの間違いをやってしまうことになる:
「全ての重みが等しければ、これは通常の相加平均である。」と言っているが,これは間違いである。 この間違いに導いたものは,計算式の変数記号の取り方である。 変数記号の取り方の間違いは,「相加平均」「加重平均」それぞれの連続型と対照させることで,はっきりする: |
| Up | 「平均」の定義──「加重平均」 | 作成: 2014-06-09 更新: 2014-06-13 |
 平均
平均
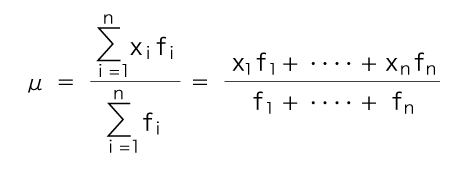
「相加平均」「加重平均」は,まったく別の概念である。 それぞれのイメージを,以下に示す:
「相加平均」と「加重平均」の本質的な意味の違いを見ないで,計算式で両者を区別しようとすると,つぎの間違いをやってしまうことになる:
「全ての重みが等しければ、これは通常の相加平均である。」と言っているが,これは間違いである。 この間違いに導いたものは,計算式の変数記号の取り方である。 変数記号の取り方の間違いは,「相加平均」「加重平均」それぞれの連続型と対照させることで,はっきりする: |