- 「関数 F: x├─→ F(x) のグラフGとしての曲線を解析」
- 曲線の解析として,関数 F: x├─→ F(x) のグラフGを解析する。
- 「接線」の意味
点 ( x, F(x) ) においてGが局所的に直線 (「なめらか」) であるとき,この直線を ( x, F(x) ) におけるGの接線と呼ぶ。
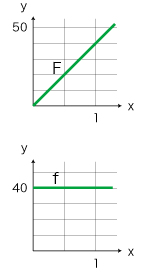
- 1次関数のグラフは直線である。
グラフ上の各点Pにおいて,グラフそれ自体が点Pにおける接線になる。
- 関数 F のグラフGが,この上のすべての点でなめらか (「いたるところなめらか」) であるとする。
このとき,つぎの関数が導かれる:
f : x├─→ 点 ( x, F(x) ) でのGの接線の傾き
f を「F の導関数」と呼ぶ。
- 1次関数の導関数は定値関数である。
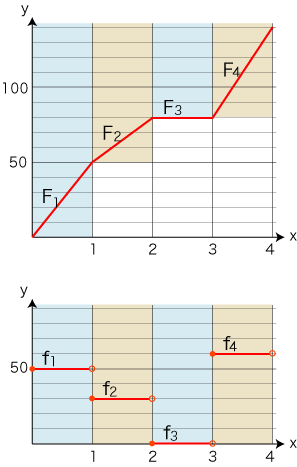
- グラフが折れ線の関数 F の導関数 f は,階段関数である。
──ただし,( a, F(a) ) が折れ線の角(かど) で,( a, F(a) ) から ( b, F(b) ) までが直線であるとき,この直線の傾きを f(a) と定めることにする。
|