- 線型変換 (「一次変換」とも言う) は,小学算数で勉強した「量の倍」の拡張ないし一般化です。
小学校では,量のカテゴリーとして「長さ」「重さ」「時間」等々が主題になりました。
このときの個々の量カテゴリーが,線型空間 (「ベクトル空間」とも言う) になります。
そして,例えば「長さ」の場合なら,個々の長さ (量) がベクトル (線型空間の要素) になります。
さらに,量の倍が,線型変換になります。
なお,「線型変換」と紛れやすい概念に「線型写像」があります。
これは,小学算数で勉強した「2量間の比例関係 (関数)」に対応します。
( 「数と量」と「線型代数」の対応表) 「数と量」と「線型代数」の対応表)
- 高校数学で主題になる「ベクトル」は,平面上の変位 (移動) です。
これは,矢線の絵で表現されます:

特に,平面上の変位全体の集合 (矢線全体の集合) が,このときの「線型空間 (ベクトル空間)」になります。
平面上の矢線に対しては,これを「量」と定め「数による倍」を考えることができます。このときの「数」は複素数です。
つまり,平面上の矢線に対しては,「量と数」と「線型空間と線型変換」の二つの扱いができます。──注意:両者は異なる概念です。
- ここで,「矢線の数表現」へと考えを進めます。
(数で表現することによって計算が可能になるからです。)
矢線の数表現はつぎのようにします:
- 矢線を一つ,「単位」として定める。── これをuとする。
u の +90度回転になる矢線を,vとする。
- 任意の矢線 z は,uxa + vxb の形に表せる。
──このときの実数の対 (a, b) を,矢線zの表現とする。
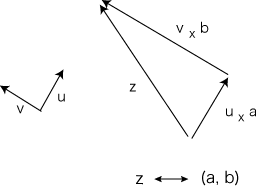
z ←→ (a, b)
これにより,実数の対を要素にする線型空間 (ベクトル空間) が得られます。
実数の対が「ベクトル」というわけです。
- そして仕上げとして,ベクトル (a, b) の図表示を導入します。
すなわち,ベクトル z の表現 (a, b) をさらに進めて,xy平面上の座標 (a, b) の点に表現します:
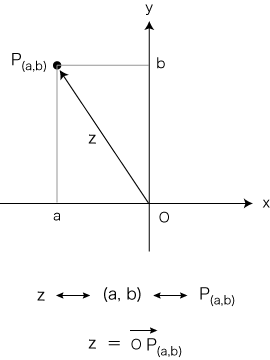
このように表現した線型空間に対する線型変換が,高校数学で主題になる「一次変換」です。
|





