「集合」は,数学のどの分野でも,基礎概念になる。
そこに「集合」が書かれていなくとも,集合は暗黙に措定されている。
「集合」の概念の指導は,「集合」をどの程度明示的にするかの違いはあるが,しばしば避けられないものになる。
例えば「関数」の概念の指導がそうである。
「集合」の概念の指導は,「集合」の概念が基礎概念であるゆえの難しさがある。
実際,基礎概念は,定義の遡行がそこで行き詰まるところであり,したがってアタリマエとして暗黙的に扱われることになるものであるから,これを改めて定立するというようなことは難しい。
(ブルバキ『数学言論』において「集合」がどのように定義されているか,見よ!)
「集合」の概念指導は,「色」とか「虫」とか「美しい」とかの概念指導と似てくる。
また,授業設計者は,「集合」の初心者であるから,単純なことが躓き・失敗のもとになる。
「集合」という用語からして,躓き・失敗のもとになる。
数学の「集合」に,「集まる・合わさる」の意味はない。
──ちなみに,「集合」の英語は「set」である。
「集合」の概念指導は,構造的に,つぎのようになる:
- これから「集合」をいろいろつくるために,それの母体となる<集合>を一つ定める。
この<集合>は,要素が明確なものでなければならない。
初心者は,だいたいが「日常的な事物・事象」で,そして一般名詞 (類概念) を用いて,「集合」を考えたがる。
「色」とか「くだもの」とか「国」といったぐあいである。
これらは,「集合」の素材にはならない。
実際,集合を確定できないわけである。
- この<集合>の要素を用いて,集合をいろいろにつくる。
併せて,集合にならない例を,いろいろ挙げる。
- 「集合」のことばの導入は,上の作業の後にくるものである。
作業中は,「グループ」のような日常語を用いることになる。
そして,つぎのような言い回しで「集合」のことばを導入するわけである:
「"グループ"という言い方をしてきたが,数学はこれを「集合」という。」
さらに,「要素」のことばを導入する。
- これで「集合」の概念のとらえがなったかというと,そうではない。
一つの<集合>に対し,「集合」を説明したに過ぎないからである。
そこで「練習」と称して,<集合>を別のものに替え,上と同じことを行う。
「集合」の概念のとらえが確実になるまで,<集合>の取り替えを行う。
- 以上の作業では,集合の数学的絵図として「ベン図」を導入することになる。
ベン図は,閉曲線である。
これに集合の名前を添えるときは,つぎのようになる:
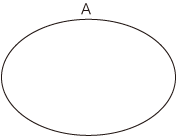
一方,「集合」の初心者はだいたいがつぎように書きたがる――これは間違いである:
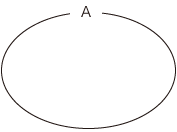
- 「集合」の概念のとらえがなったら,つぎは集合の関係概念である「交わる」や「含む」の概念の導入である。
「集合間には<交わる・含む>の関係を考えることができる」を指導する。
これも,いろいろな<集合>を用いて行う。
「いろいろ」の意味は何か?
一般概念は一つの例でわかるものではないということである。
しかし,授業の初心者は,生徒を自分とイコールにする者である。
自分の意識に上らないアタリマエが相手にとっては学習内容であるということがわからない。
そこで,一つをやってすべて教えたつもりになる。
一事が万事,こうである。
自戒すべし。
- もしこれよりさらに進むとすれば,集合の「合併」「交わり」がつぎの主題になる。
|

