数学は,規範学である。
数学は,ひとが「現象」と呼ぶものの「写し」ではない。
数学は,ひとがそれでもって「現象」をつくるようになるところの,言語・規範をつくる。
実際,数学は,《出発点にするルールを定め,これの含意を導く》を専ら行う。
<外部>は,(少なくとも理念的には) この行為の要素ではない。
そして以上の意味で,<数は量の比>は数学である。
この内容を,以下見ていくことにする。
「数・量」の数学化は,結果的にはつぎのプロセスになっている:
- 「数」の概念化の端緒は,日常語で「量」と呼ぶもの (個数,長さ,重さ,時間,移動,‥‥) 。
- この「量」を担うものを,数学的に形式化する:
| 集合 |
 | とか |  | とか |
|
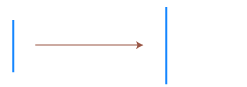
| 線分 |
 | とか |  | とか |
|
1次元ベクトル
(直線上自由なベクトル) |
 | とか |  | とか |
|
2次元ベクトル
(平面上自由なベクトル) |
 | とか |  | とか |
|
| ‥‥‥‥‥‥ |
- このときの「量」の比を,「数」の<意味>にする:
- <意味>を構成している形式をとりだし,この形式を「数」の<定義>にする。
- 集合,線分,1次元ベクトル,2次元ベクトル,‥‥ のそれぞれにおいて,「数」になるものを<実現>する:
- 「数」の<意味>を論ずるときに使った 集合,線分,1次元ベクトル,2次元ベクトル,‥‥ を,「不純なもの」として消し去る作業に入る。
すなわち,自然数,分数,正負の数,複素数,‥‥ のそれぞれで,つぎのことを行う ( 『「数とは何か?」への答え』): 『「数とは何か?」への答え』):
(1) 数を素材にして,「量の普遍対象」をつくる。
( (自然数,+), ×, (自然数, +, ×) )
( (分数,+), ×, (分数, +, ×) )
( (正負の数,+), ×, (正負の数, +, ×) )
( (複素数,+), ×, (複素数, +, ×) )
‥‥
(2)「量の普遍対象」に同型なもののことを「量」と定義する。
( (Q,+), ×, (自然数, +, ×) ) 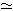 ( (自然数,+), ×, (自然数, +, ×) ) ( (自然数,+), ×, (自然数, +, ×) )
( (Q,+), ×, (分数, +, ×) ) 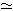 ( (分数,+), ×, (分数, +, ×) ) ( (分数,+), ×, (分数, +, ×) )
( (Q,+), ×, (正負の数, +, ×) ) 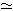 ( (正負の数,+), ×, (正負の数, +, ×) ) ( (正負の数,+), ×, (正負の数, +, ×) )
( (Q,+), ×, (複素数, +, ×) ) 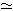 ( (複素数,+), ×, (複素数, +, ×) ) ( (複素数,+), ×, (複素数, +, ×) )
‥‥
ここで「不純なもの」の意味は,これを無くさないと循環論法になるということ。
──実際,量を担わせられた集合,線分,1次元ベクトル,2次元ベクトル,‥‥ は,数を構成要素に含むものになっている。
以上の過程を済ませて,数学は,形式としての「数」「量」を論ずるものになる。
「数」については,これの実現として,自然数,分数,正負の数,複素数,‥‥ をもっている。
一方,「量」については,<存在>をもっていない。
参考:『「数とは何か?」への答え』
|












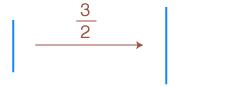
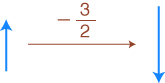
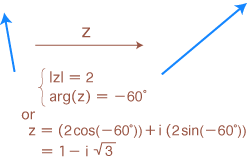
 『「数とは何か?」への答え』
『「数とは何か?」への答え』 ( (自然数,+), ×, (自然数, +, ×) )
( (自然数,+), ×, (自然数, +, ×) )