先ず,これを行う。 <液体の体積(かさ) と重さの関係>を例にする。 この関係は,比例関係である。 体積(系) と重さ(系) を,分数係数で考えよう。 分数(系) を (N, +, ×) とし,体積(系),重さ(系) をそれぞれ ( (Q体積, +), ×, (N, +, ×) ), ( (Q重さ, +), ×, (N, +, ×) ) とする。 ──なお,この構造の普遍対象が,<量としての数>の ( (N, +), ×, (N, +, ×) ) である。 「比例関係」は,数学では,「量の構造に関する準同型」ということになる。 そして数学の表記にならえば,体積(系) と重さ(系) の間の比例関係全体の集合は,Hom( Q体積, Q重さ) と書かれる。 Hom( Q体積, Q重さ) からは,量 ( (Hom( Q体積, Q重さ), +), ×, (N, +, ×) ) が導かれる。 すなわち,+ と × を,つぎのように定義するわけである: こうして,比例関係は量になる。 例えば,速度は時間と距離の比例関係であるが,これは量として足したり倍したりできるわけであり,実際,日常的にそうしている。
以上で,「1あたり量 × いくつ分」に対する「<比例関係>と<量>の結合」の解釈を示す準備ができた。 「1あたり量 × いくつ分」は,「×」の意味を,Hom( Q体積, Q重さ) × Q体積 の Q重さ への写像:
すなわち,つぎを記号「×」の用法にしている:
(  「2個/皿 × 3皿 = 6個」の数学:テンソル積) 「2個/皿 × 3皿 = 6個」の数学:テンソル積)
「数の積は量の積の抽象」の意味は,<f × x に対し,数の積の式を立てる>である。 これをどのようにしているか? 文章題では,体積と重さの単位がたとえば cm3 と g で与えられ,そして f × x が「 2/5 g/cm3 × 4/3 cm3」のようになる。 「数の積は量の積の抽象」の立場は,「 2/5 g/cm3 × 4/3 cm3」に対し直接「2/5 × 4/3」を立式することになる。 ここには,明証は無い。 これを明証する数学は,つぎのようになる:
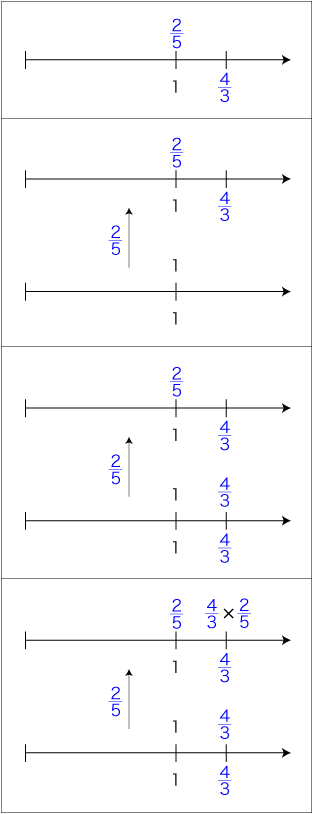
「数直線」だと,つぎの手順の作図になる:
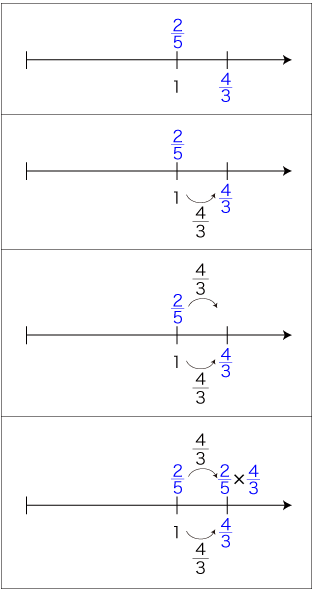
ここで,「1あたり量 × いくつ分」での 2/5 と 4/3 の順序が,数の積の式では逆になった。 「1あたり量 × いくつ分」の順序と積の式の2数の順序を同じにしたいならば,g/cm3 × 2/5 が比例関係であることを先に適用して,つぎの流れに替えることになる:
このように,「<比例関係>と<量>の結合」の解釈を以て「1あたり量 × いくつ分」を立場とするときは,数の積の式での2数の順序が定まらない。 「1あたり量 × いくつ分」を立場にすることは,「<比例関係>と<量>の結合」がこれの解釈である場合には,「かけ算に順序はない」を引き受けることなのである。 |