Up 「１あたり量 × いくつ分」 作成: 2012-02-04
更新: 2012-02-04

    学校数学の「数」は，＜数は量の抽象＞である。
    例えば，分数「2/3」は，つぎの絵に表現されるものになる：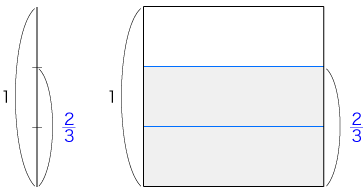


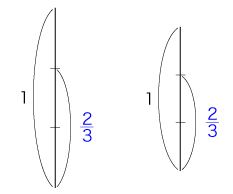
    実際には，つぎの二つの「2/3」を並べてみればわかるように，「2/3」は量を表しているのではなく，量の比を表している：


    すなわち，こういうことである：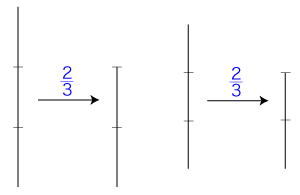


    ＜数は量の抽象＞の無理な立場は，「かけ算」の意味づけでいっきょに苦しいものになる。
    数が量の抽象だとすると，数の積は量の積の抽象でなければならない。
    たとえば，「2/3 × 4/5」をどう考えたらよいか？
    つぎのようだと，意味が立たない：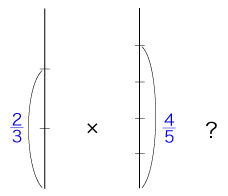


    ＜数は量の抽象＞はここで，つぎの理屈を出してくる：
    「 かけ算は，１あたり量 × いくつ分 である。
    １あたり量，いくつ分 は，異なるタイプの量 (内包量と外延量) であるが，いずれにしても量である。
    というわけで，数はやはり量の抽象であり，そして数の積は量の積の抽象である。    」

    数学は，＜数は量の比＞である。
    ＜数は量の抽象＞と＜数は量の比＞を対比すると，つぎのようになる：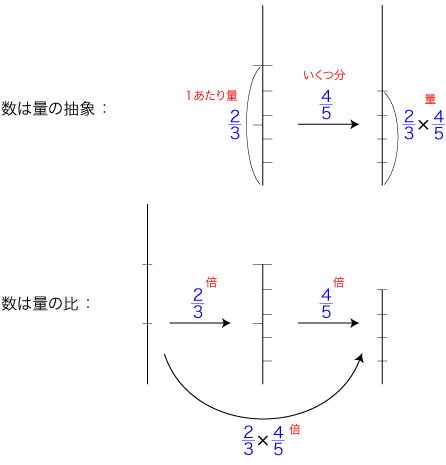


    しかし，学校数学が数学と見なしているのは，＜数は量の抽象＞の図式の方である。